
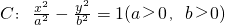 ,则
,则 是直线l与双曲线C恰有一个公共点的
是直线l与双曲线C恰有一个公共点的 解:当“直线l与双曲线C有且只有一个公共点”成立时有可能是直线与双曲线的渐近线平行,或直线与双曲线相切,如图.
解:当“直线l与双曲线C有且只有一个公共点”成立时有可能是直线与双曲线的渐近线平行,或直线与双曲线相切,如图. 不一定成立;
不一定成立; ”成立,即“直线l与双曲线C的渐近线平行”,一定能推出“直线l与双曲线C有且只有一个公共点”
”成立,即“直线l与双曲线C的渐近线平行”,一定能推出“直线l与双曲线C有且只有一个公共点” ”是“直线l与双曲线C恰有一个公共点“的充分不必要条件.
”是“直线l与双曲线C恰有一个公共点“的充分不必要条件.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 2 |
| b |
| 2 |
| a |
| b |
| CA |
| BD |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2009年辽宁省大连市高考数学一模试卷(理科)(解析版) 题型:解答题
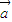 =(x-2,
=(x-2,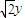 ),
),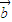 =(x+2,
=(x+2,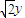 )且
)且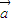 •
•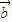 =0
=0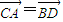
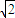 ,1),求△NCD面积取得最大时直线l的方程.
,1),求△NCD面积取得最大时直线l的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com