
分析 (1)将函数f(x)化简,转化为二次函数问题,即可求解出实数a的值;
(2)f(x)>m(cosx+1)恒成立,转化为cos2x+acosx-mcosx>m-2.令cos2x+acosx-mcosx为新函数g(x)求解a=2,且当x∈[0,$\frac{π}{2}$]时的最小值,即可得实数m的取值范围.
解答 解:(1)∵函数f(x)=cos2x+acosx+2=2cos2x+acosx+1=2(cosx+$\frac{a}{4}$)2+1-$\frac{{a}^{2}}{8}$.
∵a>0,且当x∈R时,f(x)的最小值为-1,
∴当cosx=-$\frac{a}{4}$时,f(x)min=1-$\frac{{a}^{2}}{8}$=-1,解得a=4.
(2)由题意,f(x)>m(cosx+1)恒成立,
即cos2x+acosx-mcosx>m-2.
令cos2x+acosx-mcosx=g(x)
当a=2时,g(x)=2cos2x-1+2cosx-1-mcosx=2cos2x+(2-m)cosx+1=2(cosx-$\frac{m-2}{4}$)2+1-$\frac{(m-2)^{2}}{8}$
当x∈[0,$\frac{π}{2}$]时,cosx∈[0,1].
若:0≤$\frac{m-2}{4}$≤1,即:2≤m≤6时,g(x)的最小值为:1-$\frac{(m-2)^{2}}{8}$>m-2.
可得:$6-2\sqrt{6}$<m<6+2$\sqrt{6}$.
∴可得实数m的取值范围是:2≤m≤6.
若:$\frac{m-2}{4}$<0,即:2>m时,g(x)的最小值为:2(0-$\frac{m-2}{4}$)2+1-$\frac{(m-2)^{2}}{8}$>m-2.
可得:m<3.
∴可得实数m的取值范围是:m<2.
若:$\frac{m-2}{4}$>1,即:6<m时,g(x)的最小值为:2(1-$\frac{m-2}{4}$)2+1-$\frac{(m-2)^{2}}{8}$>m-2.
可得:m<$\frac{7}{2}$.
∴m无解
综合可得:实数m的取值范围是:(-∞,6].
点评 本题考查考查三角函数值、诱导公式、三角函数的周期、单调区间等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=8,b=16,A=30° | B. | b=18,c=20,B=60° | C. | a=15,b=2,A=90° | D. | a=4,b=3,A=120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4:5:6 | B. | 3:5:7 | C. | 4:6:8 | D. | 3:5:6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 21 | C. | 34 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
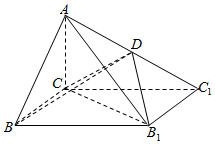 如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.
如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com