
 (x≠-1)的反函数,Sn为数列{an}的前n项和,a1=1,且f-1(Sn+1)=Sn(n∈N*).
(x≠-1)的反函数,Sn为数列{an}的前n项和,a1=1,且f-1(Sn+1)=Sn(n∈N*). }是等差数列;
}是等差数列; |,Tn是数列{bn}的前n项和,求Tn.
|,Tn是数列{bn}的前n项和,求Tn.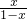 (x≠1).
(x≠1). ,即
,即 ,
, }是以1为公差,首项为1的等差数列.…(4分)
}是以1为公差,首项为1的等差数列.…(4分) ,即Sn=
,即Sn= .
. =-
=-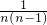 ,
, …(6分)
…(6分) …(7分)
…(7分) ,
, }是以1为公差,首项为1的等差数列,由等差数列的定义得证.
}是以1为公差,首项为1的等差数列,由等差数列的定义得证.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
| 10x+a | 10x+1 |
查看答案和解析>>
科目:高中数学 来源:设计必修一数学(人教A版) 人教A版 题型:044
已知函数f(x)=-![]() x2-3x-
x2-3x-![]() .
.
(1)求图象的开口方向、对称轴、顶点坐标、与x轴的交点坐标;
(2)求函数的单调区间、最值和零点;
(3)设图象与x轴相交于(x1,0)、(x2,0),不求出根,求|x1-x2|;
(4)已知f(-![]() )=
)=![]() ,不计算函数值,求f(-
,不计算函数值,求f(-![]() );
);
(5)不计算函数值,试比较f(-![]() )与f(-
)与f(-![]() )的大小;
)的大小;
(6)写出使函数值为负数的自变量x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
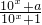 是奇函数.
是奇函数.查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求图象的开口方向、对称轴、顶点坐标、与x轴的交点坐标;
(2)求函数的单调区间、最值和零点;
(3)设图象与x轴相交于(x1,0)、(x2,0),不求出根,求|x1-x2|;
(4)已知f(-![]() )=
)=![]() ,不计算函数值,求f(-
,不计算函数值,求f(-![]() );
);
(5)不计算函数值,试比较f(-![]() )与f(-
)与f(-![]() )的大小;
)的大小;
(6)写出使函数值为负数的自变量x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 是偶函数,a为实常数.
是偶函数,a为实常数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com