(2006广州模拟)如图所示，在一个木制的棱长为3的正方体的表面涂上颜色，将它的棱3等分，然后从等分点把正方体锯开，得到27个棱长为1的小正方体，将这小正方体充分混合后，装入一个口袋中．

(1)从这个口袋中任意取出1小正方体，这个小正方体的表面恰好没涂颜色的概率是多少?

(2)从这个口袋中同时任意取出2个小正方体，其中1个小正方体恰好有1个面涂有颜色，另1个小正方体至少有2个面涂有颜色的概率是多少?

某会议室用五盏照明灯，每盏灯各使用灯泡一只，且型号相同．假定每盏灯能否正常照明只与灯泡的寿命有关，该型号的灯泡寿命为1年以上的概率为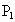，寿命为2年以上的概率为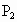，从使用之日起每满一年进行一次灯泡更换工作，只更换已坏的灯泡，平时不换．

(1)在第一次灯泡更换工作中，求不需要更换灯泡的概率和更换两只灯泡的概率．

(2)求在第二次灯泡更换工作中，对其中的某一盏灯来说，该盏灯需要更换灯泡的概率．

(3)当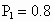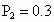，时，求在第二次灯泡更换工作中，至少需要更换4只灯泡的概率(结果保留两位有效数字)．

甲、乙两人参加普法知识竞赛，共有10个不同的题目，其中选择题6个，判断题4个，甲、乙两人依次各抽一题：

(1)甲抽到选择题，乙抽到判断题的概率是多少?

(2)甲、乙两人中至少有1人抽到选择题的概率是多少?

(2006北京，18)某公司招聘员工，指定三门考试课程，有两种考试方案．

假设某应聘者对三门指定课程考试及格的概率分别是a，b，c，且三门课程考试是否及格相互之间没有影响．

(1)分别求该应聘者用方案一和方案二时考试通过的概率；

(2)试比较该应聘者在上述两种方案下考试通过的概率的大小(说明理由)．

(山东实验中学模拟)设曲线在点处的切线为l．

(1)求直线l的方程；

(2)若直线l与x轴、y轴所围成的三角形面积为S(t)，求S(t)的最大值．

(2007北京海淀模拟)如图所示，在直角坐标系中，O为坐标原点，直线AB⊥x轴于点C，，，动点M到直线AB的距离是它到点D的距离的2倍．

(1)求点M的轨迹方程；

(2)设点K为点M的轨迹与x轴正半轴的交点，直线l交点M的轨迹于E，F两点(E，F与点K不重合)，且满足，动点P满足，求直线KP的斜率的取值范围．

(2007北京崇文模拟)如图所示，已知双曲线C的中心点为坐标原点O，焦点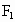、在x轴上，点P在双曲线的左支上，点M在右准线上，且满足，．

(1)求双曲线C的离心率e；

(2)若双曲线C过点Q(2，)，、是双曲线虚轴的上、下端点，点A、B是双曲线上不同的两点，且，，求直线AB的方程．

(2007上海春，17)求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题．

例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”．求出体积后，它的一个“逆向”问题可以是“若正四棱锥底面边长为4，体积为，求侧棱长”；也可以是“若正四棱锥的体积为，求所有侧面面积之和的最小值”．

试给出问题“在平面直角坐标系xOy中，求点P(2，1)到直线3x＋4y=0的距离”的一个有意义的“逆向”问题，并解答你所给出的“逆向”问题．

(山东青岛模拟)已知向量a=(cosα，sinα)，，．

(1)若，求α的值；

(2)若向量，求(a－c)·b的最大值．

(南通中学模拟)已知A、B、C三点的坐标分别为A(3，0)、B(0，3)、C(cosα，sinα)，．

(1)若，求角α的值；

(2)若，求的值．