
科目: 来源:北京师大附中2011-2012学年高一上学期期末考试数学试题 题型:044
已知| |=1,|
|=1,|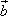 |=2,
|=2,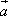 与
与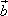 的夹角为60°.
的夹角为60°.
(1)求: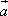 ·
·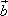 ,(
,( -
-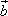 )·(
)·(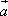 +
+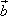 );
);
(2)求:| -
- |.
|.
查看答案和解析>>
科目: 来源:北京市师大附中2011-2012学年高二上学期期中考试数学试题 题型:044
已知方程x2+y2-2x-4y+m=0,
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于A、B两点,且OA⊥OB(O为坐标原点),求m的值;
(3)在(2)的条件下,求以AB为直径的圆的方程.
查看答案和解析>>
科目: 来源:北京市师大附中2011-2012学年高二上学期期中考试数学试题 题型:044
已知圆C:(x-3)2+(y-4)2=4和直线l:kx-t+3-4k=0,
(1)求证:不论k取什么值,直线和圆总相交;
(2)求k取何值时,直线被圆截得的弦最短,并求出最短弦的长;
查看答案和解析>>
科目: 来源:北京市师大附中2011-2012学年高二上学期期中考试数学试题 题型:044
已知点P(2,0),及⊙C:x2+y2-6x+4y+4=0.
(Ⅰ)当直线l过点P且与圆心C的距离为1时,求直线l的方程;
(Ⅱ)设过点P的直线与⊙C交于A、B两点,当|AB|=4,求以线段AB为直径的圆的方程.
查看答案和解析>>
科目: 来源:北京市师大附中2011-2012学年高二上学期期中考试数学试题 题型:044
已知圆C经过两点A(1,-1)和B(-1,1),且圆心在直线x+y-2=0上.
(Ⅰ)求圆C的方程;
(Ⅱ)若以圆C为底面的等边圆锥(轴截面为正三角形),求其内接正方体的棱长.
查看答案和解析>>
科目: 来源:北京市四中2011-2012学年高二上学期期中考试数学试题 题型:044
动圆C的方程为x2+y2+2ax-4ay+5=0.
(1)若a=2,且直线y=3x与圆C交于A,B两点,求弦长|AB|;
(2)求动圆圆心C的轨迹方程;
(3)若直线y=kx-2k与动圆圆心C的轨迹有公共点,求k的取值范围.
查看答案和解析>>
科目: 来源:北京市四中2011-2012学年高二上学期期中考试数学试题 题型:044
已知Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-![]() ),顶点C在x轴上.
),顶点C在x轴上.
(1)求BC边所在直线的方程;
(2)圆M为Rt△ABC外接圆,其中M为圆心,求圆M的方程;
(3)直线l与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程.
查看答案和解析>>
科目: 来源:北京市四中2011-2012学年高二上学期期中考试数学试题 题型:044
已知O为坐标原点,△AOB中,边OA所在的直线方程是y=3x,边AB所在的直线方程是![]() ,且顶点B的横坐标为6.
,且顶点B的横坐标为6.
(1)求△AOB中,与边AB平行的中位线所在直线的方程;
(2)求△AOB的面积;
(3)已知OB上有点D,满足△AOD与△ABD的面积比为2,求AD所在的直线方程.
查看答案和解析>>
科目: 来源:重庆市万州二中2011-2012学年高二上学期期中考试数学理科试题(人教版) 题型:044
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.

(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E-DF-C的余弦值;
(3)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
查看答案和解析>>
科目: 来源:重庆市万州二中2011-2012学年高一上学期期中考试数学试题(人教版) 题型:044
对于定义域为D的函数y=f(x),若同时满足下列条件:①f(x)在D内单调递增或单调递减;②存在区间[a,b]![]() D,使f(x)在[a,b]上的值域为[a,b];那么把y=f(x)(x∈D)叫闭函数.
D,使f(x)在[a,b]上的值域为[a,b];那么把y=f(x)(x∈D)叫闭函数.
(1)求闭函数y=-x3符合条件②的区间[a,b];
(2)判断函数f(x)=![]() x+
x+![]() (x>0)是否为闭函数?并说明理由;
(x>0)是否为闭函数?并说明理由;
(3)若函数y=k+![]() 是闭函数,求实数k的取值范围
是闭函数,求实数k的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com