如图，平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E、F、G分别是线段PA，PD，CD的中点．

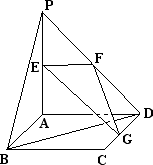
(1)求证：PB∥面EFG；

(2)求异面直线EG与BD所成的角；

(3)在线段CD上是否存在一点Q，使得点A到平面EFQ的距离为0.8．若存在，求出CQ的值；若不存在，请说明理由．

某校设计了一个实验学科的实验考查方案：考生从6道备选题中一次性随机抽取3题，按照题目要求独立完成全部实验操作．规定：至少正确完成其中2题的便可通过．已知6道备选题中考生甲有4题能正确完成，2题不能完成；考生乙每题正确完成的概率都为，且每题正确完成与否互不影响．

(1)分别写出甲、乙两考生正确完成题数的概率分布列，并计算其数学期望；

(2)试用统计知识分析比较两考生的实验操作能力．

已知△ABC的面积为，．

(1)求tanA的值；

(2)求的值．

已知函数和点P(1，0)，过点P作曲线y＝f(x)的两条切线PM、PN，切点分别为M、N．

(Ⅰ)设｜MN｜＝g(t)，试求函数g(t)的表达式；

(Ⅱ)是否存在t，使得M、N与A(0，1)三点共线．若存在，求出t的值；若不存在，请说明理由．

(Ⅲ)在(Ⅰ)的条件下，若对任意的正整数n，在区间内总存在m＋1个实数a₁，a₂，…，a_m，a_m＋1，使得不等式g(a₁)＋g(a₂)＋…＋g(a_m)＜g(a_m+1)成立，求m的最大值．

已知数列{a_n}满足：a₁＝1，，且[3＋(－1)ⁿ]a_n+2－2a_n＋2[(－1)ⁿ－1]＝0，n∈N^*．

(Ⅰ)求a₃，a₄，a₅，a₆的值及数列{a_n}的通项公式；

(Ⅱ)设b_n＝a_2n－1·a_2n，求数列{b_n}的前n项和S_n；

一束光线从点F₁(－1，0)出发，经直线l：2x－y＋3＝0上一点P反射后，恰好穿过点F₂(1，0)．

(Ⅰ)求点F₁关于直线l的对称点的坐标；

(Ⅱ)求以F₁、F₂为焦点且过点P的椭圆C的方程；

(Ⅲ)设直线l与椭圆C的两条准线分别交于A、B两点，点Q为线段AB上的动点，求点Q到F₂的距离与到椭圆C右准线的距离之比的最小值，并求取得最小值时点Q的坐标．

如图，已知正三棱柱ABC－A₁B₁C₁的底面边长是2，D是侧棱CC₁的中点，直线AD与侧面BB₁C₁C所成的角为45°．

(Ⅰ)求此正三棱柱的侧棱长；

(Ⅱ)求二面角A－BD－C的大小；

(Ⅲ)求点C到平面ABD的距离．

在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x、y，记．

(Ⅰ)求随机变量的最大值，并求事件“取得最大值”的概率；

(Ⅱ)求随机变量的分布列和数学期望．

已知，

(Ⅰ)求tanx的值；(Ⅱ)求的值．

以数列{a_n}的任意相邻两项为坐标的点P_n(a_n，a_n+1)(n∈N)均在一次函数y＝2x＋k的图象上，数列{b_n}满足条件：b_n＝a_n+1－a_n(n∈N，b₁≠0)，

(1)求证：数列{b_n}是等比数列；

(2)设数列{a_n}，{b_n}的前n项和分别为S_n，T_n，若S₆＝T₄，S₅＝－9，求k的值．