已知点C为圆的圆心，点A(1，0)，P是圆上的动点，点Q在圆的半径CP上，且·＝0，＝2．

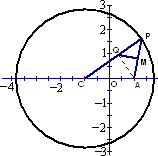
(1)当点P在圆上运动时，求点Q的轨迹方程；

(2)若直线与(1)中所求点Q的轨迹交于不同两点F、H，O是坐标原点，且·时，求△FOH面积的取值范围．

　　班主任为了对本班学生的考试成绩进行分析，决定从全班25名女同学，15名男同学中随机抽取一个容量为8的样本进行分析．

　　(Ⅰ)如果按性别比例分层抽样，可以得到多少个不同的样本？(只要求写出算式即可，不必计算出结果)；

　　(Ⅱ)随机抽取8位，他们的数学分数从小到大排序是：60、65、70、75、80、85、90、95，物理分数从小到大排序是：72、77、80、84、88、90、93、95．

(1)若规定85分以上(包括85分)为优秀，求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率；

(2)若这8位同学的数学、物理分数事实上对应如下表：

根据上表数据用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间是否具有线性相关性？如果具有线性相关性，求y与x的线性回归方程(系数精确到0.01)，如果不具有线性相关性，请说明理由．

如图，四棱锥P－ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA＝PB＝1，AD＝，点F是PB的中点，点E在边BC上移动．

(1)点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；

(2)证明：无论点E在BC边的何处，都有PE⊥AF；

(3)当BE等于何值时，PA与平面PDE所成角的大小为45°．

设向量．

(1)若，求tanx的值；

(2)求函数·的最大值及相应x的值．

如图四棱锥P－ABCD的底面为正方形，PA⊥平面ABCD，AB＝2，PC与平面ABCD成45°角，E、F分别为PA、PB的中点．

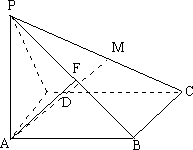
(1)求异面直线DE与AF所成角的大小；

(2)设M是PC上的动点，试问当M在何处时，才能使AM⊥平面PBD，证明你的结论．

一个四棱锥S－ABCD的底面是边长为a的正方形，侧面展开图如图(1)所示．

(1)请画出四棱锥S－ABCD的示意图，问是否存在一条

侧棱与底面垂直？若存在，请给出证明；

(2)若SC为四棱锥中最长的侧棱，点E为AB的中点．

①求二面角E－SC－D的大小；

②求点D到平面SEC的距离．

已知双曲线的中心在坐标原点，焦点在x轴上，实轴长为2．一条斜率为1的直线l过右焦点F与双曲线交于A，B两点，以AB为直径的圆与右准线交于M，N两点．

(1)若双曲线的离心率为2，求圆的半径；

(2)设AB的中点为H，若，求双曲线的方程．

已知椭圆C的方程为，双曲线的两条渐近线为l₁，l₂，过椭圆C的右焦点F作直线l，使l⊥l₁，又l与l₂交于P，设l与椭圆C的两个交点由上至下依次为A、B(如图)．

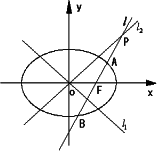
(1)当l₁与l₂的夹角为60°，且△POF的面积为时，求椭圆C的方程；

(2)当时，求的最大值．

设椭圆E：的左、右焦点分别为F₁，F₂，已知椭圆E上的任意一点P，满足，过F₁作垂直于椭圆长轴的弦长为3．

(1)求椭圆E的方程；

(2)若过F₁的直线交椭圆于A，B两点，求的取值范围．

在直角坐标平面上，O为原点，N为动点，｜｜＝6，．过点M作MM₁⊥y轴于M₁，过N作NN₁⊥x轴于点N₁，＝＋，记点T的轨迹为曲线C．

(Ⅰ)求曲线C的方程；

(Ⅱ)已知直线L与双曲线C₁：5x²－y²＝36的右支相交于P、Q两点(其中点P在第一象限)，线段OP交轨迹C于A，若＝3，S_ΔPAQ＝－26tan∠PAQ，求直线L的方程．