设F是抛物线G：x²＝4y的焦点．

(Ⅰ)过点P(0，－4)作抛物线G的切线，求切线方程：

(Ⅱ)设A、B为势物线G上异于原点的两点，且满足，延长AF、BF分别交抛物线G于点C，D，求四边形ABCD面积的最小值．

如下图，在六面体ABCD－A₁B₁C₁D₁中，四边形ABCD是边长为2的正方形，四边形A₁B₁C₁D₁是边长为1的正方形，DD₁⊥平面A₁B₁C₁D₁，DD₁⊥平面ABCD，

DD₁＝2．

(Ⅰ)求证：与共面

(Ⅱ)求证：平面A₁ACC₁⊥平面B₁BDD₁；

(Ⅲ)求二面角A－BB₁－C的大小(用反三角函数值表示)．

解不等式(|3x－1|－1)(sinx－2)＞0．

已知{a_n}是等差数列，(b_n)是公比为q的等比数列，a₁＝b₁，a₂＝b₂≠a₁，记S_n为数列{b_n}的前n项和，

(1)若b_k＝a_m(m，k是大于2的正整数)，求证：S_k－1＝(m－1)a₁；

(2)若b₃＝a_i(i是某一正整数)，求证：q是整数，且数列{b_n}中每一项都是数列{a_n}中的项；

(3)是否存在这样的正数q，使等比数列{b_n}中有三项成等差数列？若存在，写出一个q的值，并加以说明；若不存在，请说明理由；

如下图，在平面直角坐标系xOy中，过y轴正方向上一点C(0，c)任作一直线，与抛物线y＝x²相交于AB两点，一条垂直于x轴的直线，分别与线段AB和直线l∶y＝－c交于P，Q，

(1)若，求c的值；

(2)若P为线段AB的中点，求证：QA为此抛物线的切线；

(3)试问(2)的逆命题是否成立？说明理由．

如下图，已知ABCD－A₁B₁C₁D₁是棱长为3的正方体，点E在AA₁上，点F在CC₁上，且AE＝FC₁＝1，

(1)求证：E，B，F，D₁四点共面；

(2)若点G在BC上，，点M在BB₁上，GM⊥BF，垂足为H，求证：EM⊥面BCC₁B₁；

(3)用θ表示截面EBFD₁和面BCC₁B₁所成锐二面角大小，求tanθ．

某气象站天气预报的准确率为80%，计算(结果保留到小数点后面第2位)

(1)5次预报中恰有2次准确的概率；

(2)5次预报中至少有2次准确的概率；

(3)5次预报中恰有2次准确，且其中第3次预报准确的概率；

如图，中心在原点O的椭圆的右焦点为F(3，0)，右准线l的方程为：x＝12．

(1)求椭圆的方程；

(2)在椭圆上任取三个不同点P₁，P₂，P₃，使∠P₁FP₂＝∠P₂FP₃＝∠P₃FP₁，证明

为定值，并求此定值．

已知各项均为正数的数列{a_n}的前n项和满足S_n＞1，且

6S_n＝(a_n＋1)(a_n＋2)，n∈N^*

(1)求{a_n}的通项公式；

(2)设数列{b_n}满足，并记T_n为{b_n}的前n项和，求证：

3T_n＋1＞log₂(a_n＋3)，n∈N^*

如图，在直三棱柱ABC－A₁B₁C₁中，AA₁＝2，∠ABC＝90°AB＝1；点D、E分别在上，且B₁E⊥A₁D，四棱锥C－ABDA₁与直三棱柱的体积之比为3∶5．■

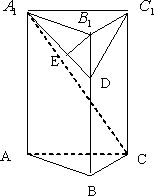
(1)求异面直线DE与B₁C₁的距离；

(2)若BC＝，求二面角A₁－DC₁－B₁的平面角的正切值．