已知点P_n(a_n，b_n)(n∈N^*)都在直线l：y＝2x＋2上，P₁为直线l与x轴的交点，数列{a_n}成等差数列，公差为1．

(Ⅰ)求数列{a_n}，{b_n}的通项公式；

(Ⅱ)若f(n)＝问是否存在k∈N^*，使得f(k＋5)＝2f(k)－5成立？若存在，求出k的值，若不存在，说明理由；

(Ⅲ)求证：(n≥2，n∈N^*)．

已知函数f(x)＝x²＋a1nx．

(Ⅰ)当a＝－2时，求函数f(x)的单调区间和极值；

(Ⅱ)若函数在[1，＋∞)上是增函数，求实数a的取值范围．

已知A、B两点的坐标分别为AB其中．

(Ⅰ)求的表达式；

(Ⅱ)若(O为坐标原点)，求tanx的值；

(Ⅲ)若(λ∈R)，求函数f(x)的最小值．

已知函数(t∈R，a＜0)的最大值为正实数，集合，集合B＝{x｜x²＜b²}．

(1)求A和B；

(2)定义A与B的差集：A－B＝{x｜x∈A}且．设a，b，x均为整数，且x∈A．P(E)为x取自A－B的概率，P(F)为x取自A∩B的概率，写出a与b的二组值，使，．

(3)若函数f(t)中，a，b是(2)中a较大的一组，试写出f(t)在区间[，m]上的最大值函数g(m)的表达式．

如图，设抛物线C：x²＝4y的焦点为F，P(x₀，y₀)为抛物线上的任一点(其中x₀≠0)，过P点的切线交y轴于Q点．

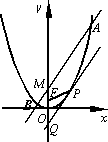
(1)证明：｜FP｜＝｜FQ｜；

(2)Q点关于原点O的对称点为M，过M点作平行于PQ的直线交抛物线C于A、B两点，若(λ＞1)，求λ的值．

已知数列{a_n}的前n项和为S_n，对一切正整数n，点P_n(n，S_n)都在函数f(x)＝x²＋2x的图象上，且过点P_n(n，S_n)的切线的斜率为k_n．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若，求数列{b_n}的前n项和为T_n；

(Ⅲ)设Q＝{x｜x＝k_n，n∈N^*}，R＝{x｜x＝2a_n，n∈N^*}，等差数列{c_n}的任一项c_n∈Q∩R，其中c₁是Q∩R中的最小数，110＜c₁₀＜115，求{c_n}的通项公式．

如图，O是半径为1的球心，点A、B、C在球面上，OA、OB、OC两两垂直，E、F分别是大圆弧AB与AC的中点，

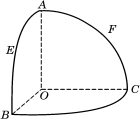
⑴求点E、F在该球面上的球面距离；

⑵求平面OEF与平面OBC所成的锐二面角．(用反三角函数表示)

若函数f(x)＝sin²ax－sinaxcosax(a＞0)的图象与直线y＝m(m为常数)相切，并且切点的横坐标依次成公差为的等差数列．

(Ⅰ)求m的值；

(Ⅱ)若点A(x₀，y₀)是y＝f(x)图象的对称中心，且x₀∈[0，]，求点A的坐标．

某次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并且宣布：观众答对问题A可获奖金a元，答对问题B可获奖金2a元；先答哪个题由观众自由选择；只有第1个问题答对，才能再答第2个问题，否则中止答题．若你被选为幸运观众，且假设你答对问题A、B的概率分别为、．你觉得应先回答哪个问题才能使你获得奖金的期望较大？说明理由．

如图，设抛物线C：x²＝4y的焦点为F，P(x₀，y₀)为抛物线上的任一点(其中x₀≠0)，过P点的切线交y轴于Q点．

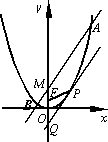
(1)证明：｜FP｜＝｜FQ｜；

(2)Q点关于原点O的对称点为M，过M点作平行于PQ的直线交抛物线C于A、B两点，若(λ＞1)，求λ的值．