数列{a_n}满足，已知a₃＝95．

(1)求a₁，a₂；

(2)是否存在一个实数t，使得且{b_n}为等差数列？若存在，则求出t的值；若不存在，请说明理由．

设函数f(x)＝x³＋ax²＋bx＋c，过曲线y＝f(x)上的点P(1，f(1))的切线方程为y＝3x＋1．

(1)若y＝f(x)在x＝－2时有极值，求f(x)的表达式；

(2)在(1)的条件下，求y＝f(x)在[－3，1]上的最大值．

如图，在长方体ABCD－A₁B₁C₁D₁中，AD＝AA₁＝1，AB＝2，点E是棱AB上的动点．

(1)证明：D₁E⊥A₁D；

(2)若二面角D₁－EC－D为45°时，求EB的长．

在人寿保险业中，要重视某一年龄的投保人的死亡率，经过随机抽样统计，得到某城市1个投保人能活到75岁的概率为0.60，试问：

(1)3个投保人都能活到75岁的概率；

(2)3个投保人中只有1人能活到75岁有概率；

(3)3个投保人中至少有1人能活到75岁的概率．

在△ABC中，，BC＝1，．

(1)求sinA的值；

(2)求的值．

定义函数其导函数记为_．

(1)求证：f_n(x)≥nx；

(2)设，求证：0＜x₀＜1；

(3)是否存在区间使函数h(x)＝f₃(x)－f₂(x)在区间[a，b]上的值域为[ka，kb]？若存在，求出最小的k值及相应的区间[a，b]．

把正整数按上小下大，左小右大的原则排成三角形数表示(每一行比上一行多一个数)，如下图所示：设是位于这个三角形数表中从上往下数第i行，从左往右数第j个数，如a₄₂＝8．

(1)若a_ij＝2007，求i，j的值；

(2)记三角形数表从上往下数第n行各数之和为b_n，令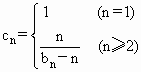，若数列{c_n}的前n项和为T_n，求的值．

如图：半径为2的圆，在外力下压成椭圆，圆心“弹开”，半径裂成两条(长度不变)，

(1)求椭圆的标准方程；

(2)过该椭圆外一点M，连接与AM，分别交椭圆于不同两点与P，且与P关于x轴对称，求点M的轨迹方程．

在湖南卫视的一次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并且宣布：幸运观众答对问题A可获奖金1000元，答对问题B可获奖金2000元，先答哪个题由观众自由选择，但只有第一个问题答对，才能再答第二题，否则终止答题．若你被选为幸运观众，且假设你答对问题A、B的概率分别为、．

(1)记先回答问题A的奖金为随机变量ξ，则ξ的取值分别是多少？

(2)你觉得应先回答哪个问题才能使你获得更多的奖金？请说明理由．

已知△ABC的面积S满足3≤S≤3，且·＝6，与的夹角为α

(1)求α的取值范围；

(2)若函数f(α)＝sin²α＋2sinαcosα＋3cos²α，求f(α)的最小值．