如图，已知正三棱柱ABC－A₁B₁C₁的底面边长是2，D是侧棱CC₁的中点，直线AD与侧面BB₁C₁C所成的角为45°．

求(Ⅰ)求此正三棱柱的侧棱长；

(Ⅱ)求二面角A－BD－C的大小；

(Ⅲ)求点C到平面ABD的距离．

对于三次函数f(x)＝ax³＋bx²＋cx＋d(a≠0)

定义：(1)设(x)是函数y＝f(x)的导数y＝(x)的导数，若方程(x)＝0有实数解x₀，则称点为函数y＝f(x)的“拐点”；

定理：(2)设x₀为常数，若定义在R上的函数y＝f(x)对于定义域内的一切实数x，都有f(x₀＋x)＋f(x₀－x)＝2f(x₀)成立，则函数y＝f(x)的图象关于点对称．

己知f(x)＝x³－3x²＋2x＋2

求：(Ⅰ)求函数f(x)的“拐点”A的坐标

(Ⅱ)检验函数f(x)的图象是否关于“拐点”A对称，对于任意的三次函数写出一个有关“拐点”的结论(不必证明)

(Ⅲ)写出一个三次函数G(x)，使得它的“拐点”是(－1，3)(不要过程)

如图所示，已知圆C：(x＋1)²＋y²＝8，定点A(1，0)，M为圆上一动点，点P在AM上，点N在C上，且满足，＝0，点N的轨迹为曲线E．

(I)求曲线E的方程；

(II)若过定点F(0，2)的直线交曲线E于不同的两点G、H(点G在点F、H之间)，且满足，求λ的取值范围．

已知函数f(x)＝ax²＋lnx，

(1)当a＝－时，求函数在f(x)[1，e]上的最大值、最小值；

(2)求f(x)的单调区间；

如图，P－ABCD是正四棱锥，ABCD－A₁B₁C₁D₁是正方体，

其中AB＝2，PA＝．

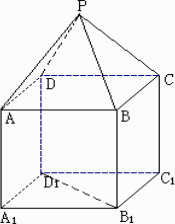
(1)求证：PA⊥B₁D₁；

(2)求平面PAD与平面BDD₁B₁所成的锐二面角θ的大小；

(3)求B₁到平面PAD的距离．

甲、乙两人各射击一次，击中目标的概率分别是和．假设两人射击是否击中目标，相互之间没有影响；每人各次射击是否击中目标，相互之间也没有影响．

⑴求甲射击4次，至少1次未击中目标的概率；

⑵假设某人连续2次未击中目标，则停止射击．问：乙恰好射击5次后，被中止射击的概率是多少？

⑶用ξ表示甲击中目标时射击的次数，求ξ的数学期望Eξ

已知锐角△ABC中，角A、B、C的对边分别为a，b，c，且tanB＝；

(1)求∠B；

(2)求函数f(x)＝sinx＋2sinBcosx　　(x)的最大值

(文)设数列{a_n}的前n项和S_n＝，n＝1，2，3……

(1)求数列{a_n}的通项公式a_n．

(2)求数列{}的前n项和T_n．

(文)一袋中装有分别标记着1、2、3、4、5数字的5个球

(1)从袋中一次取出3个球，试求三个球中最大数字为4的概率．

(2)从这袋中每次取出1个球，取出后放回，连续取三次，试求取出的三个球中最大数字为4的概率．

一袋中装有分别标记着1、2、3、4数字的4个球，从这只袋中每次取出1个球，取出后放回，连续取三次，设三次取出的球中数字最大的数为ξ．

(1)求ξ＝3时的概率；

(2)求ξ的概率分布列及数学期望．