已知函数．

(Ⅰ)若函数的值；

(Ⅱ)设的充分条件，求实数m的取值范围．

已知函数f(x)满足ax·f(x)＝b＋f(x)，(a·b≠0)，f(1)＝2且f(x＋2)＝－f(2－x)对定义域中任意x都成立．

(1)求函数f(x)的解析式；

(2)若数列{a_n}的前n项和为S_n，{a_n}满足当n＝1时，a₁＝f(1)＝2，当n≥2时，，试给出数列{a_n}的通项公式，并用数学归纳法证明．

设函数，其图象在点A(1，f(1))，B(m，f(m))处的切线的斜率分别为0，－a．

(Ⅰ)求证：；

(Ⅱ)若函数f(x)的递增区间为[s，t]，求|s－t|的取值范围；

(Ⅲ)若当x≥k时(k是与a，b，c无关的常数)，恒有(x)＋a＜0，试求k的最小值．

已知一次函数f(x)的图象关于直线x－y＝0对称的图象为C，且f[f(1)＝－1]，若点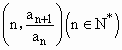在曲线C上，并有．

①求f(x)的解析式及曲线C的方程；

②求数列{a_n}的通项公式；

③设，求的值．

如图，在底面是菱形的四棱锥P－ABCＤ中，∠ABC＝60°，PA＝AC＝a，PB＝PD＝，点E在PD上，且PE∶ED＝2∶1．

(Ⅰ)证明PA⊥平面ABCD；

(Ⅱ)求以AC为棱，EAC与DAC为面的二面角的大小；

(Ⅲ)在棱PC上是否存在一点F，使BF∥平面AEC？证明你的结论．

在湖南卫视的一次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并且宣布：幸运观众答对问题A可获奖金1000元，答对问题B可获奖金2000元，先答哪个题由观众自由选择，但只有第一个问题答对，才能再答第二题，否则终止答题．若你被选为幸运观众，且假设你答对问题A、B的概率分别为、．

(1)记先回答问题A的奖金为随机变量ζ，则ζ的取值分别是多少？

(2)你觉得应先回答哪个问题才能使你获得更多的奖金？请说明理由．

已知函数f(x)＝ax＋b，当x∈[a₁，b₁]时，f(x)的值域为[a₂，b₂]，当x∈[a₂，b₂]时，f(x)的值域为[a₃，b₃]，…，当x∈[a_n－1，b_n－1]时，f(x)的值域为[a_n，b_n]，其中a，b为常数，a₁＝0，b₁＝1．

(Ⅰ)a＝1时，求数列{a_n}与{b_n}的通项；

(Ⅱ)设a＞0且a≠1，若数列{b_n}是公比不为1的等比数列，求b的值；

(Ⅲ)若a＞0，设{a_n}与{b_n}的前n项和分别记为S_n与T_n，求：(T₁＋T₂＋…＋T_n)－(S₁＋S₂＋…＋S_n)的值．

某工厂生产一种仪器的元件，由于受生产能力和技术水平的限制，会产生一些次品，根据经验知道，其次品率P与日产量x(万件)之间大体满足关系：

(其中c为小于6的正常数)

(注：次品率＝次品数/生产量，如P＝0.1表示每生产10件产品，有1件为次品，其余为合格品)

已知每生产1万件合格的仪器可以盈利2万元，但每生产1万件次品将亏损1万元，故厂方希望定出合适的日产量．

(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数

(2)当日产量为多少时，可获得最大利润？

在△ABC中，a，b，c分别为角A，B，C的对边，且a，b，c成等比数列．

(Ⅰ)求∠B的范围；

(Ⅱ)求的取值范围．

设向量，，其中．

(Ⅰ)求的取值范围；

(Ⅱ)若函数的大小