玻璃球盒中装有各色球12只，其中5红、4黑、2白、1绿．

(1)从中取1个球，求取得红或黑的概率；

(2)从中取2个球，求至少一个红球的概率．

设数列{a_n}满足a₁＝a，a_n+1＝ca_n＋1－c，n∈N^＊其中a，c为实数，且c≠0，a≠1，

(1)求证{a_n－1}是等比数列．

(2)求数列{a_n}的通项公式

(3)设，b_n＝n(1－a_n)，n∈N^＊，求证数列{b_n}的前n项和S_n＜2．

△ABC中，角A、B、C所对的边分别是a，b，c，且角B、A、C成等差数列

(1)求的值；

(2)若，求bc的最大值．

在△ABC中，BC＝a，AC＝b，a，b是方程的两个根，且2cosc＝－1

求(1)角C的度数；

(2)AB的长；

(3)△ABC的面积．

已知数列{a_n}的前n项和为S_n，且a₁＝2，3S_n＝5a_n－a_n－1＋3S_n－1，(n∈N，n≥2)

求(1)数列{a_n}的通项公式；

(2)若b_n＝(2n－1)a_n，求数列{b_n}的前n项和T_n．

如图所示，已知圆C：(x＋1)²＋y²＝8，定点A(1，0)，M为圆上一动点，点P在AM上，点N在CM上，且满足AM＝2AP，NP⊥AM，点N的轨迹为曲线E．

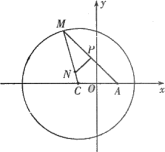
(1)求曲线E的方程；

(2)若过定点F(0，2)的直线l交曲线E于不同的两点G、H(点G在点F、H之间)，且满足，求直线l的方程；

(3)设曲线E的左右焦点为F₁，F₂，过F₁的直线交曲线于Q，S两点，过F₂的直线交曲线于R，T两点，且QS⊥RT，垂足为W；(ⅰ)设W(x₀，y₀)，证明：；(ⅱ)求四边形QRST的面积的最小值．

设有两个命题：p：关于x的不等式x²＋|2x－4|－a≥0对一切x∈R恒成立；q：已知a≠0，a≠±1，函数y=－|a|^x在R上是减函数，若p∧q为假命题，p∨q为真命题．求实数a的取值范围．

在甲、乙两个盒子中分别装有标号为1、2、3、4、5的五个球，现从甲、乙两个盒子中各取出1个球，每个小球被取出的可能性相等．

(1)求事件“取出的两个球上标号为相邻整数”的概率；

(2)求事件“取出的两个球上标号之和能被3整除”的概率；

已知双曲线的中心在原点，一条渐近线方程为，焦点在坐标轴上，两准线之间的距离为，求双曲线的标准方程．

如图是总体的一样本频率分布直方图，且在[15，18)内的频数为8，

求：(1)样本容量；

(2)若在[12，15)内小矩形面积为0.06，求在[12，15)内的频数；

(3)在(2)的条件下，求样本数据在[18，33)内的频率并估计总体数据在[18，33)内的频率．