某校高二两个班学生的数学成绩表如下：

问：两班的数学成绩有差别吗？

为了研究患慢性气管炎与吸烟量的关系，调查了228人，其中每天的吸烟支数在10支以上20支以下的调查者中，患者人数有98人，非患者人数有89人；每天的吸烟支数在20支以上的调查者中，患者人数有25人，非患者人数有16人，试问患慢性气管炎是否与吸烟量相互独立？

如图，F是椭圆＝1(a＞b＞0)的一个焦点，A、B是椭圆的两个顶点，椭圆的离心率为，点C在x轴上，BC⊥BD，B，C，F三点确定的圆M恰好与直线x＋y＋3＝0相切．

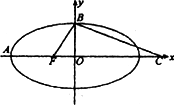
(Ⅰ)求椭圆的方程；

(Ⅱ)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点，在x轴上是否存在点N，使得NF恰好为△PNQ的内角平分线，若存在，求出点N的坐标，若不存在，请说明理由．

如图，四面体ABCD中，O是BD的中点，△ABD和△BCD均为等边三角形，AB＝2，AC＝．

(Ⅰ)求证：AO⊥平面BCD；

(Ⅱ)求二面角A－BC－D的余弦值；

(Ⅲ)求O点到平面ACD的距离．

已知函数f(x)＝ax⁴1nx＋bx⁴－c(x＞0)在x＝1处取得极值－3－c，其中a，b，c为常数，

(1)试确定a，b的值；

(2)讨论函数f(x)的单调区间；

(3)若对任意x＞0，不等式f(x)≥－2c²恒成立，求c的取值范围．

某村计划建造一个室内面积为800 m²的矩形蔬菜温室．在温室内，沿左．右两侧与后侧内墙各保留1 m宽的通道，沿前侧内墙保留3 m宽的空地．当矩形温室的边长各为多少时？蔬菜的种植面积最大？最大种植面积是多少？

某服装批发商场经营的某种服装，进货成本40元/件，对外批发价定为60元/件．该商场为了鼓励购买者大批量购买，推出优惠政策：一次购买不超过50件时，只享受批发价；一次购买超过50件时，每多购买1件，购买者所购买的所有服装可在享受批发价的基础上，再降低0.1元/件，但最低价不低于50元/件．

(1)问一次购买多少件时，售价恰好是50元/件？

(2)设购买者一次购买x件，商场的利润为y元(利润＝销售总额－成本)，试写出函数y＝f(x)的表达式．并说明在售价高于50元/件时，购买者一次购买多少件，商场利润最大．

已知集合A＝{x|x²－3x＋2＝0}，B＝{x|x²＋ax＋a＋3＝0}，若BA，求实数a的取值范围．

设全集U＝{1，2，3，4}，且A＝{x|x²－5x＋m＝0}，若A＝{2，3}，求m的值．

已知f(x＋2)＝x²－3x＋5．

(1)求f(x)的解析式；

(2)求f(x)在闭区间[t，t＋1](t∈R)上的最大值．