经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为：．

(1)在该时段内，当汽车的平均速度v为多少时，车流量最大？最大车流量为多少？

(保留分数形式)

(2)若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？

意大利数学家菲波拉契，在1202年出版的一书里提出了这样的一个问题：一对兔子饲养到第二个月进入成年，第三个月生一对小兔，以后每个月生一对小兔，所生小兔能全部存活并且也是第二个月成年，第三个月生一对小兔，以后每月生一对小兔．问这样下去到年底应有多少对兔子？试画出解决此问题的程序框图．

长方体ABCD－A₁B₁C₁D₁中，AB＝BC＝1，AA₁＝2，E是侧棱BB₁中点．

(1)求直线AA₁与平面A₁D₁E所成角的大小；

(2)求二面角E－AC₁－B的正切值大小；

(3)求三棱锥A－C₁D₁E的体积．

已知P是直线3x＋4y＋8＝0上的动点，PA，PB是圆x²＋y²－2x－2y＋1＝0的两条切线，A，B是切点，C是圆心，求：四边形PACB面积的最小值．

设圆上的点A(2，3)关于直线x＋2y＝0的对称点仍在圆上，且与直线x－y＋1＝0相交的弦长为2，求圆的方程．

如图所示，在直四棱柱ABCD－A₁B₁C₁D₁中，已知DC＝DD₁＝2AD＝2AB，AD⊥DC，AB∥DC．

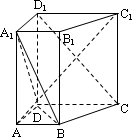
(Ⅰ)求证：D₁C⊥AC₁；

(Ⅱ)设E是DC上一点，试确定E的位置，使D₁E∥平面A₁BD，并说明理由．

如图所示，已知P为菱形ABCD外一点，PA⊥平面ABCD，∠ABC＝60°，E，F分别是BC，PC的中点．

(1)证明：AE⊥PD；

(2)若H为PD上的动点，EH与平面PAD所成最大角的正切值为，求二面角E－AF－C的余弦值．

如图所示，PA⊥平面ABCD，四边形ABCD是矩形，PA＝AD＝a，M，N分别是AB，PC的中点．

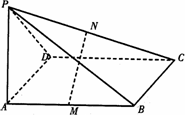
(1)求平面PCD与平面ABCD所成二面角的大小；

(2)求证：MN⊥平面PCD；

(3)当AB的长度变化时，求异面直线PC与AD所成角的可能范围．

如图1所示，已知矩形ABCD，AB＝2AD＝2a，E是CD边的中点，以AE为棱，将△DAE向上折起，将D变到的位置，使面AE与面ABCE成直二面角(图2)．

(1)求直线B与平面ABCE所成的角的正切值；

(2)求证：A⊥BE；

(3)求点C到平面AE的距离．

如图所示，在五面体P－ABCD中，底面ABCD是平行四边形，∠BAD＝60°，AB＝4，AD＝2，PB＝，PD＝．

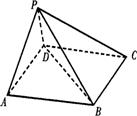
(1)求证：BD⊥平面PAD；

(2)若PD与底面ABCD成60°的角，试求二面角P－BC－A的大小．