
科目: 来源: 题型:044
(
山东实验中学模拟)如图所示,已知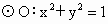 和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(1)
求实数a,b间满足的等量关系;(2)
求线段PQ长的最小值;(3)
若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程.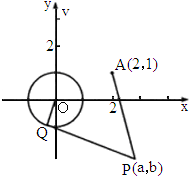
查看答案和解析>>
科目: 来源: 题型:044
(2007
广州模拟)已知 ,直线l∶y=kx,且l与圆C相交于P、Q两点,点M(0,b),且MP⊥MQ.
,直线l∶y=kx,且l与圆C相交于P、Q两点,点M(0,b),且MP⊥MQ.
(1)
当b=1时,求k的值:(2)
当 时,求k的取值范围.
时,求k的取值范围.查看答案和解析>>
科目: 来源: 题型:044
(2006
北京海淀模拟)已知A(-2,0)、B(2,0),点C、D满足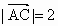 ,
,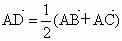 .
.
(1)
求点D的轨迹方程;(2)
过点A作直线l交以A、B为焦点的椭圆于M、N两点,线段MN的中点到y轴的距离为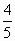 ,且直线l与点D的轨迹相切,求该椭圆的方程.
,且直线l与点D的轨迹相切,求该椭圆的方程.查看答案和解析>>
科目: 来源: 题型:044
如图所示,半径为
1的圆C过原点O,Q为圆C与x轴的另一个交点,OQRP为平行四边形,其中RP为圆C的切线,P为切点,且P点在x轴上方,当圆C绕原点O旋转时,求R点的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:044
(2007
全国Ⅱ,20)在直角坐标系xOy中,以O为圆心的圆与直线 相切.
相切.
(1)
求圆O的方程;(2)
圆O与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求 的取值范围.
的取值范围.查看答案和解析>>
科目: 来源: 题型:044
(2008
上海春,22)已知z是实数方程 的虚根,记它在直角坐标平面上的对应点为
的虚根,记它在直角坐标平面上的对应点为 .
.
(1)
若(b,c)在直线2x+y=0上,求证: 在圆
在圆 上;
上;
(2)
给定圆 ,则存在唯一的线段s满足:①若
,则存在唯一的线段s满足:①若 在圆C上,则(b,c)在线段s上;②若(b,c)是线段s上一点(非端点),则
在圆C上,则(b,c)在线段s上;②若(b,c)是线段s上一点(非端点),则 在圆C上.写出线段s的表达式,并说明理由;
在圆C上.写出线段s的表达式,并说明理由;
(3)
由(2)知线段s与圆C之间确定了一种对应关系,通过这种对应关系的研究,填写表一[表中 是(1)中圆
是(1)中圆 的对应线段].
的对应线段].
表一

查看答案和解析>>
科目: 来源: 题型:044
(2007
苏锡常镇四市模拟)如图所示,已知点D在定线段MN上,且|MD|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M,N作圆C的另两条切线交于点P.(1)
建立适当的直角坐标系,求点P的轨迹方程;(2)
过点M作直线l与所求轨迹交于两个不同的点A,B,若 ,且
,且 ,求直线l与直线MN夹角θ的取值范围.
,求直线l与直线MN夹角θ的取值范围.

查看答案和解析>>
科目: 来源: 题型:044
(2006
北京朝阳模拟)如图所示,已知圆 ,设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
,设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
(1)
当r=2时,求满足条件的P点的坐标;(2)
当r (1,+∞)时,求点N的轨迹G的方程;
(1,+∞)时,求点N的轨迹G的方程;
(3)
过点P(0,2)的直线l与(2)中轨迹G相交于两个不同的点E、F,若 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.

查看答案和解析>>
科目: 来源: 题型:044
(
山东师大附中模拟)某民营企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图甲,B产品的利润与投资的算术平方根成正比,其关系如图乙(注:利润与投资单位:万元).
(1)
分别将A、B两种产品的利润表示为投资x(万元)的函数关系式;(2)
该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com