某观测站C在城A的南偏西20°方向上，从城A出发有一条公路，走向是南偏东40°，在距C处31公里的公路上的B处有一个人正沿着公路向城A走去，走20公里后到达D处，测得CD＝21公里，求这时此人距城A多少公里？某同学甲已经由余弦定理求得．

设F₁，F₂分别是椭圆的左、右焦点，过F₁斜率为1的直线l与E相交于A，B两点，且|AF₂|，|AB|，|BF₂|成等差数列．

(Ⅰ)求E的离心率；

(Ⅱ)设点P(0，－1)满足|PA|＝|PB|，求E的方程．

在平面直角坐标系xOy中，点P(a，b)(a＞b＞0)为动点，F₁、F₂分别为椭圆的左右焦点，已知△F₁PF₂为等腰三角形．

(Ⅰ)求椭圆的离心率e；

(Ⅱ)设直线PF₂与椭圆相交于A，B两点，M是直线PF₂上的点，满足·＝－2，求点M的轨迹方程．

在△ABC中，角A，B，C所对的边分别为a，b，c．已知sinA＋sinC＝psinB(p∈R)，且

(1)当，时，求a，c的值；

(2)若角B为锐角，求p的取值范围．

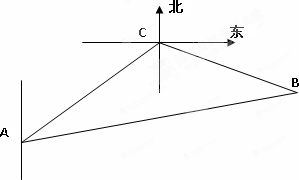
一缉私艇在A处发现在其北偏东45°方向，距离12 nmile的海面C处有一走私船正以10 nmile/h的速度沿东偏南15°方向逃窜．缉私艇的速度为14 nmile/h，若要在最短的时间内追上该走私船，缉私艇应沿北偏东45°＋α的方向去追，求追及所需的时间和α角的正弦值．

如图所示，F₁、F₂分别为椭圆C：的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点P到F₁、F₂两点的距离之和为4．

(1)求椭圆C的方程；

(2)过椭圆C的焦点F₂作AB的平行线交椭圆于P、Q两点，求△F₁PQ的面积．

已知椭圆的离心率为，过右焦点F的直线l与C相交于A、B两点，当l的斜率为1时，坐标原点O到l的距离为．

(Ⅰ)求a，b的值；

(Ⅱ)C上是否存在点P，使得当l绕F转到某一位置时，有＝＋成立？若存在，求出所有的P的坐标与l的方程；若不存在，说明理由．

如图，三棱柱ABC－A₁B₁C₁中，底面为正三角形，侧棱与底面垂直，D是BC的中点，AA₁＝AB＝1．

(1)求证：A₁C∥平面AB₁D；

(2)求点C到平面AB₁D的距离．