
科目: 来源: 题型:044
(2005
全国I,20)9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为0.5.若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没有发芽,则这个坑需要补种.假定每个坑至多补种一次,每次种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望(精确到0.01).查看答案和解析>>
科目: 来源: 题型:044
(2006
天津,12)某射手进行射击训练,假设每次射击击中目标的概率为 ,且各次射击的结果互不影响.
,且各次射击的结果互不影响.
(1)
求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)
求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)
设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.查看答案和解析>>
科目: 来源: 题型:044
(
东北师大附中模拟)一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求:(1)
连续取两次都是红球的概率;(2)
如果取出黑球,则取球终止,否则继续取球,直到取出黑球,但取球次数最多不超过4次,求取球次数ξ的概率分布列及期望.查看答案和解析>>
科目: 来源: 题型:044
(
唐山五校模拟)甲、乙、丙、丁四人独立破解一类数据,甲、乙二人能独立破解成功的概率都是 ,丙、丁二人能独立破解成功的概率都是
,丙、丁二人能独立破解成功的概率都是 ,今由4人同时破解这类数据,求:
,今由4人同时破解这类数据,求:
(1)
数据不能被破解的概率;(2)
破解成功的人数ξ的分布列和期望.查看答案和解析>>
科目: 来源: 题型:044
(2007
天津,18)已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.(1)
求取出的4个球均为黑球的概率;(2)
求取出的4个球中恰有1个红球的概率;(3)
设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望.查看答案和解析>>
科目: 来源: 题型:044
(2007
黄冈模拟)如下图,在直三棱柱 中,BA=BC=2,
中,BA=BC=2, ,异面直线
,异面直线 与AC成60°的角,点O、E分别是棱AC和
与AC成60°的角,点O、E分别是棱AC和 的中点,点F是棱
的中点,点F是棱 上的动点.
上的动点.
(1)
证明: ⊥OF;
⊥OF;
(2)
求点E到面 的距离;
的距离;
(3)
求二面角 的大小.
的大小.

查看答案和解析>>
科目: 来源: 题型:044
(2006
四川,19)如下图,在长方体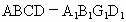 中,E、P分别是BC、
中,E、P分别是BC、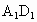 的中点,M、N分别是AE、
的中点,M、N分别是AE、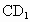 的中点,
的中点,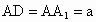 ,AB=2a.
,AB=2a.
(1)
求证:MN∥面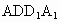 ;
;
(2)
求二面角P-AE-D的大小:(3)
求三棱锥P-DEN的体积.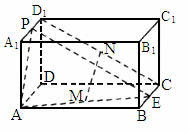
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com