
科目: 来源: 题型:044
(
唐山五校模拟)如下图,四棱锥P-ABCD的底面是直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3.PC=CD=2,PC⊥底面ABCD,E为AB的中点.(1)
求证:平面PDE⊥平面PAC;(2)
求直线PC与平面PDE所成的角;(3)
求点B到平面PDE的距离.
查看答案和解析>>
科目: 来源: 题型:044
(2006
北京崇文模拟)已知正四棱柱ABCD- 中,底面边长为
中,底面边长为 ,侧棱长为4,点E、F分别是棱AB、BC中点,EF与BD相交于G,如下图.
,侧棱长为4,点E、F分别是棱AB、BC中点,EF与BD相交于G,如下图.
(1)
求异面直线 和DC所成的角;
和DC所成的角;
(2)
求证:平面 ⊥平面
⊥平面 ;
;
(3)
求点 到平面
到平面 的距离.
的距离.

查看答案和解析>>
科目: 来源: 题型:044
(2007
北京朝阳模拟)如下图,棱长为1的正四面体ABCD中,E、F分别是棱AD、CD的中点,D是点A在平面BCD内的射影.(1)
求直线EF与直线BC所成角的大小;(2)
求点O到平面ACD的距离;(3)
求二面角A-BE-F的大小.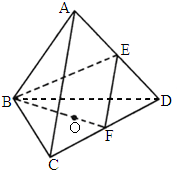
查看答案和解析>>
科目: 来源: 题型:044
(2007
全国Ⅱ,19)如图所示,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点.(1)
证明:EF∥平面SAD;(2)
设SD=2DC,求二面角A-EF-D的大小.
查看答案和解析>>
科目: 来源: 题型:044
(2004
湖北,18)如下图,在棱长为1的正方体ABCD- 中,AC与BD交于点E,
中,AC与BD交于点E, 与
与 交于点F.
交于点F.
(1)
求证: ⊥平面
⊥平面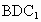 ;
;
(2)
求二面角B-EF-C的大小(结果用反三角函数值表示).
查看答案和解析>>
科目: 来源: 题型:044
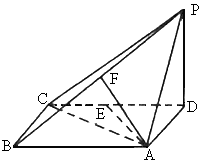
(2005
全国Ⅱ,20)如下图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点.(1)
求证:EF⊥平面PAB;(2)
设AB=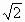 BC,求AC与平面AEF所成的角的大小.
BC,求AC与平面AEF所成的角的大小.
查看答案和解析>>
科目: 来源: 题型:044
(
娄底联考模拟)如下图,在四棱锥P-ABCD中.底面ABCD为直角梯形,且AB∥CD,AB⊥AD,AD=CD=2AB=2.侧面△PAD为正三角形,且平面PAD⊥平面ABCD.(1)
若M为PC上一动点,则M在何位置时,PC⊥平面MDB?并加已证明;(2)
若G为△PBC的重心,求二面角G-BD-C的大小.
查看答案和解析>>
科目: 来源: 题型:044
(
皖南八校模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点,(1)
求证:AF∥平面PEC;(2)
求PC与平面ABCD所成角的大小;(3)
求二面角P-EC-D的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com