某公司拟资助三位大学生自主创业，现聘请两位专家，独立地对每位大学生的创业方案进行评审．假设评审结果为“支持”或“不支持”的概率都是．若某人获得两个“支持”，则给予10万元的创业资助；若只获得一个“支持”，则给予5万元的资助；若未获得“支持”，则不予资助．求：

(1)该公司的资助总额为零的概率；

(2)该公司的资助总额超过15万元的概率．

设函数f(x)＝|x－1|＋|x－a|．

(1)若a＝－1解不等式f(x)≥3；

(2)如果，f(x)≥2，求α的取值范围．

坐标系与参数方程在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρcos()＝1，M，N分别为C与x轴，y轴的交点．

(1)写出C的直角坐标方程，并求M，N的极坐标；

(2)设MN的中点为P，求直线OP的极坐标方程．

已知ΔABC中，AB＝AC，D是ΔABC外接圆劣弧上的点(不与点A，C重合)，延长BD至E．

(1)求证：AD的延长线平分∠CDE；

(2)若∠BAC＝30，ΔABC中BC边上的高为2＋，求ΔABC外接圆的面积．

已知点P₁(x₀，y₀)为双曲线为正常数)上任一点F₂为双曲线的右焦点，过P₁作右准线的垂线，垂足为A，连接F₂A并延长交y轴于点P₂．

(1)求线段P₁P₂的中点P的轨迹F的方程；

(2)设轨迹E与x轴交于B，D两点，在E上任取一点Q(x₁，y₁)(y≠0)，直线QB，QD分别交于y轴于M，N两点．求证：以MN为直径的圆过两定点．

在四棱锥P－ABCD中ABCD是矩形，PA⊥平面ABCD，PA＝AD＝4，AB＝2．以AC为中点O为球心，AC为直径的球面交PD于点M，交PC于点N．

(1)求证：平面ABM⊥平面PCD；

(2)求直线CD与平面ACM所夹的角的大小；

(3)求点N到平面ACM的距离．

△ABC中，A，B，C所对的边分别为a，b，c，tanC＝，sin(B－A)＝cosC

(1)求A，C

(2)若s_△ABC＝3＋，求a，c．

(1)求函数f(x)的单调区间

(2)若k＞0，求不等式＞的解集．

如图，在正三棱柱ABC－A₁B₁C₁中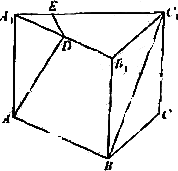，D是A₁B₁的中点，点E在A₁C₁上，且DE⊥AE．

(Ⅰ)证明平面ADE⊥平面ACC₁A₁

(Ⅱ)求直线AD和平面ABC所成角的正弦值．

在ΔABC，已知，求角A，B，C的大小．