设P₁(x₁，y₁)、P₂(x₂，y₂)是函数图象上的两点，且，点P的横坐标为．

(1)求证：P点的纵坐标为定值，并求出这个定值；

(2)若，求S_n；

(3)记T_n为数列的前n项和，若对一切都成立，试求a的取值范围．

设定义在R的函数f(x)满足：①对任意的实数x、y有f(x＋y)＝f(x)·f(y)．

②当x＞0时，f(x)＞1、数列{a_n}满足a₁＝f(0)，且f(a_n+1)＝

(1)求f(0)，并判断f(x)的单调性；

(2)求数列{a_n}的通项公式a_n

(3)令b_n是最接近的正整数，即

已知函数，点P₁(x₁，y₁)，P₂(x₂，y₂)是函数f(x)图像上的两个点，且线段P₁P₂的中点P的横坐标为．

(1)求证：点P的纵坐标是定值；

(2)若数列{a_n}的通项公式为，求数列{a_n}的前m项的和S_m；

(3)若m∈N时，不等式恒成立，求实数a的取值范围．

已知正数数列{a_n}成GP，(1)公比q＞1若m＋k＝2n，比较a_m^m＋a_k^k与2a_nⁿ大小

(2)若mk＝n²比较1°大小；2°若a₁＞q，比较大小．

对于函数f(x)，若存在，使f(x₀)＝x₀成立，则称x₀为f(x)的不动点．如果函数有且仅有两个不动点0、2，且．

(1)试求函数f(x)的单调区间；

(2)已知各项不为零的数列{a_n}满足，求证：；

(3)设，T_n为数列{b_n}的前n项和，求证：T₂₀₀₈－1＜ln2008＜T₂₀₀₇．

已知奇函数f(x)在上有意义，且在(0，＋∞)上是减函数，f(1)＝0又有函数，若集合M＝{m|g(θ)＜0}，集合N＝{m|f[g(θ)]＞0}．

(Ⅰ)求f(x)＞0的解集；

(Ⅱ)求．

设数列{a_n}的前n项和为S_n，对一切，点(n，S_n)在函数f(x)＝x²＋x的图象上．

(Ⅰ)求a_n的表达式；

(Ⅱ)将数列{a_n}依次按1项、2项、3项、4项循环地分为(a₁)，(a₂，a₃)，(a₄，a₅，a₆)，(a₇，a₈，a₉，a₁₀)；(a₁₁)，(a₁₂，a₁₃)，(a₁₄，a₁₅，a₁₆)，(a₁₇，a₁₈，a₁₉，a₂₀)；(a₂₁)，…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为{b_n}，求b₅＋b₁₀₀的值；

(Ⅲ)设A_n为数列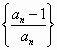的前n项积，是否存在实数a，使得不等式对一切都成立？若存在，求出a的取值范围；若不存在，请说明理由．

已知直线l的方程为x＝－2，且直线l与x轴交于点M，圆O：x²＋y²＝1与x轴交于A，B两点(如图)．

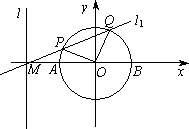
(I)过M点的直线l₁交圆于P、Q两点，且圆孤PQ恰为圆周的，求直线的方程；

(II)求以l为准线，中心在原点，且与圆O恰有两个公共点的椭圆方程；

(III)过M点的圆的切线l₂交(II)中的一个椭圆于C、D两点，其中C、D两点在x轴上方，求线段CD的长．

直三棱柱ABC－A₁B₁C₁中，∠ACB＝120°，AC＝CB＝A₁A＝1.

(Ⅰ)求证：B₁C₁∥平面A₁BC；

(Ⅱ)求三棱锥A－A₁CB的体积；

(Ⅲ)求二面角A₁－CB－A的正切值.

为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分均为整数，满分为100分)进行统计．请你根据尚未完成并有局部污损的频率分布表和频数分布直方图，解答下列问题：

(Ⅰ)填充频率分布表的空格(在答题纸上写出a，b，c，d，e的值)；

(Ⅱ)补全频数条形图；

(Ⅲ)若成绩在75.5~ 85.5分的学生为二等奖，问获得二等奖的学生约为多少人？