如图，正三棱锥O－ABC的三条侧棱OA、OB、OC两两垂直，且长度均为2．E、F分别是AB、AC的中点，H是EF的中点，过EF作平面与侧棱OA、OB、OC或其延长线分别相交于A₁、B₁、C₁，已知．

(1)求证：B₁C₁⊥平面OAH；

(2)求二面角O－A₁B₁－C₁的大小；

数列{a_n}为等差数列，a_n为正整数，其前n项和为S_n，数列{b_n}为等比数列，且a₁＝3，b₁＝1，数列是公比为64的等比数列，b₂S₂＝64．

(1)求a_n，b_n；

(2)求证．

某柑桔基地因冰雪灾害，使得果林严重受损，为此有关专家提出两种拯救果林的方案，每种方案都需分两年实施；若实施方案一，预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二，预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5；第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案，第二年与第一年相互独立．令表示方案i实施两年后柑桔产量达到灾前产量的倍数．

(1)写出的分布列；

(2)实施哪种方案，两年后柑桔产量超过灾前产量的概率更大？

(3)不管哪种方案，如果实施两年后柑桔产量达不到灾前产量，预计可带来效益10万元；两年后柑桔产量恰好达到灾前产量，预计可带来效益15万元；柑桔产量超过灾前产量，预计可带来效益20万元；问实施哪种方案所带来的平均效益更大？

若，，x∈R，p₁，p₂为常数，且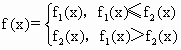

(1)求f(x)＝f₁(x)对所有实数x成立的充要条件(用p₁，p₂表示)

(2)设a，b为两实数，a＜b且p₁，p₂∈(a，b)若f(a)＝f(b)

求证：f(x)在区间[a，b]上的单调增区间的长度和为(闭区间[m，n]的长度定义为n－m)

设a₁，a₂，……a_n是各项均不为零的等差数列(n≥4)，且公差d≠0，若将此数列删去某一项得到的数列(按原来的顺序)是等比数列：

①当n＝4时，求的数值；

②求n的所有可能值．

某地有三家工厂，分别位于矩形ABCD的顶点A、B及CD的中点P处，已知AB＝20 km，BC＝10 km，为了处理三家工厂的污水，现要在矩形ABCD的区域上(含边界)，且A、B与等距离的一点O处建造一个污水处理厂，并铺设排污管道AO、BO、OP，设排污管道的总长为y km．

(1)按下列要求写出函数关系式：

①设∠BAO＝θ(rad)，将y表示成θ的函数关系式；

②设OP＝x(km)，将y表示成x的函数关系式；

(2)请你选用(1)中的一个函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短．

已知椭圆的中心在原点，一个焦点是F(2，0)，且两条准线间的距离为λ(λ＞4)．

(1)求椭圆的方程；

(2)若存在过点A(1，0)的直线l，使点F关于直线l的对称点在椭圆上，求λ的取值范围．

如图所示，四棱锥P－ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，PA⊥底面ABCD，PA＝．

(1)证明：平面PBE⊥平面PAB；

(2)求二面角A－BE－P和的大小．

已知函数．

(Ⅰ)求函数f(x)的最小正周期；

(Ⅱ)当且时，求的值．

已知函数f(x)＝ln²(1＋x)－．

(Ⅰ)求函数f(x)的单调区间；

(Ⅱ)若不等式对任意的n∈N*都成立(其中e是自然对数的底数)．求α的最大值．