为减少世博中心区域内的环境污染，有关部门决定，从2006年开始停止办理世博中心区域内摩托车入户手续．此时该区域内居民摩托车拥有量已达1.6万辆．据测算，每7辆摩托车排放污染物总量等于一辆公交车排放的污染物，而每辆摩托车的运送能力是一辆公交车运送能力的4％．若从2006年年初起n年内退役部分摩托车，第一年退役a万辆，以后每年退役的摩托车数量是上一年的80％，同时增加公交车的数量，使新增公交车的运送能力等于退役摩托车原有的运送能力．

(1)求n年内新增公交车的总量S_n(万辆)；

(2)要求到2010年年初，剩余摩托车与新增公交车排放污染物的总量不超过原有1.6万辆摩托车排放污染物总量的一半，假定每辆摩托车排放污染物数量为b，问第一年至少退役摩托车多少万辆？(精确到0.01)

如图，已知椭圆的中心在坐标原点，焦点F₁，F₂在x轴上，长轴A₁A₂的长为4，左准线l与x轴的交点为M，．

(Ⅰ)求椭圆的方程；

(Ⅱ)过点M的直线与椭圆交于C、D两点，若，求直线的方程．

(理)如图，直三棱柱A₁B₁C₁－ABC中，C₁C＝CB＝CA＝2，AC⊥CB．D、E分别为棱C₁C、B₁C₁的中点．

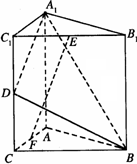
(1)求点B到平面A₁C₁CA的距离；

(2)求二面角B－A₁D－A的余弦值；

(3)在线段AC上是否存在一点F，使得EF⊥平面A₁BD？若存在，确定其位置并证明结论；若不存在，说明理由．

设P(x₁，y₁)，Q(x₂，y₂)是抛物线C：y²＝2px上相异两点，且·＝0，直线QP与x轴相交于E．

(1)若Q、P到x轴的距离的积为4，求p的值；

(2)若视p为已知常数，在x轴上，是否存在异于E的一点F，直线PF与抛物线的另一交点为R，而直线RQ与x轴相交于T，且有＝3，若存在，求出F点的坐标(用p表示)，若不存在，说明理由．

(文)已知某类学习任务的掌握程度y与学习时间t(单位时间)之间有如下函数关系：

这里我们称这一函数关系为“学习曲线”．已知这类学习任务中的某项任务有如下两组数据：t＝4，y＝50％；t＝8，y＝80％．

(1)试确定该项学习任务的“学习曲线”；

(2)计算f(0)并指出其实际含义；

(3)若定义在区间[x₁，x₂]上的平均学习效率为，问这项学习任务从哪一时刻开始的2个单位时间内平均效率最高．

如下图，已知△ABC三个角，A，B，C满足sin²B＋sin²C－sin²A＝sinB·sinC，AD是△ABC外接圆直径，CD＝2，BD＝3，求∠CAB和AD的长．

将圆x²＋y²－2x＋4y＝0按向量a＝(－1，2)平移后得到⊙O，直线l与⊙O相交于A、B两点，若在⊙O上存在点C，使＝λa，求直线l的方程及对应的点C的坐标．

已知四棱锥P－ABCD的底面为直角梯形，AB∥DC，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC＝1，AB＝2，M是PB的中点．

(Ⅰ)证明：面PAD⊥面PCD；

(Ⅱ)求AC与PB所成的角余弦值；

(Ⅲ)求面AMC与面BMC所成二面角的余弦值．

已知正项数列{a_n}满足S_n＋S_n－1＝ta＋2(n≥2，t＞0)，a₁＝1，其中S_n是数列{a_n}的前n项和．

(Ⅰ)求通项a_n；

(Ⅱ)记数列{}的前n项和为T_n，若T_n＜2对所有的n∈N^*都成立．求证：0＜t≤1．

如果函数满足f(0)＝0，f(2)＝2，且．

(Ⅰ)求函数f(x)的解析式；

(Ⅱ)是否存在各项均不为零的数列{a_n}满足(s_n为该数列的前n项和)，如果存在，写出数列的一个通项公式a_n，并说明满足条件的数列是{a_n}否唯一确定；如果不存在，请说明理由．