
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(文科数学) 题型:044
已知数列{an}的首项a1=4,前n项和为Sn,且Sn+1-3Sn-2n-4=0(n∈N*).
(1)求数列{an}的通项公式;
(2)设函数f(x)=a1x+a2x2+…+anxn,![]() (x)是函数f(x)的导函数,求
(x)是函数f(x)的导函数,求![]() (1).
(1).
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(文科数学) 题型:044
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,点M是SD的中点,AN⊥SC,且交SC于点N.

(1)求证:SB∥平面ACM;
(2)求二面角D―AC―M的大小;
(3)求证:平面SAC⊥平面AMN.
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(文科数学) 题型:044
2008年5月12日,四川汶川发生8.0级特大地震,通往灾区的道路全部中断.5月12日晚,抗震救灾指挥部决定从水路(一支队伍);陆路(东南和西北两个方向各一支队伍);空中(一支队伍)同时向灾区挺进.在5月13日,仍时有较强余震发生,天气状况也不利于空中航行.已知当天从水路抵达灾区的概率是![]() ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是![]() ,从空中抵达灾区的概率是
,从空中抵达灾区的概率是![]() .
.
(1)求在5月13日从水路或空中有队伍抵达灾区(即从水路和空中至少有一支队伍抵达灾区)的概率;
(2)求在5月13日至少有3支队伍抵达灾区的概率.
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(文科数学) 题型:044
在△ABC中,a、b、c分别为角A、B、C的对边.已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(1)求角C;
(2)若![]() ,△ABC的面积
,△ABC的面积![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(理科数学) 题型:044
已知点P在曲线C:y=![]() (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图像交于点A,与x轴交于点B,设点P的横坐标为t,设A、B的横坐标分别为xA、xB,记f(t)=xA·xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图像交于点A,与x轴交于点B,设点P的横坐标为t,设A、B的横坐标分别为xA、xB,记f(t)=xA·xB.
(Ⅰ)求f(t)的解析式;
(Ⅱ)设数列{an}(n≥1,n∈N)满足a1=1,an=f(![]() )(n≥2),数列{bn}(n≥1,n∈N)满足bn=
)(n≥2),数列{bn}(n≥1,n∈N)满足bn=![]() ,求{an}和{bn}的通项公式;
,求{an}和{bn}的通项公式;
(Ⅲ)在(Ⅱ)的条件下,当1<k<3时,证明不等式:a1+a2+a3+…+an>![]() .
.
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(理科数学) 题型:044
已知F1、F2分别是椭圆![]() =1(a>0,b>0)的左、右焦点,其左准线与x轴相交于点N,并且满足,
=1(a>0,b>0)的左、右焦点,其左准线与x轴相交于点N,并且满足,![]() .
.
(1)求此椭圆的方程;
(2)设A、B是这个椭圆上的两点,并且满足![]() 当
当![]() 时,求直线AB的斜率的取值范围.
时,求直线AB的斜率的取值范围.
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(理科数学) 题型:044
已知A、B、C是直线l上的三点,向量![]() 满足:
满足:![]() -[y+2
-[y+2![]() (1)]
(1)]![]() +ln(x+1)
+ln(x+1)![]() =
=![]()
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0,证明:f(x)>![]() ;
;
(Ⅲ)若不等式![]() x2≤f(x2)+m2-2bm-3时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2bm-3时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(理科数学) 题型:044
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°
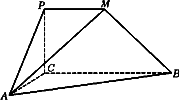
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的正切值;
(Ⅲ)求多面体P-MABC的体积.
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(理科数学) 题型:044
有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为0.5.若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.假定更换一个面需要100元,用ξ表示维修一次的费用.
(Ⅰ)求恰好有2个面需要维修的概率;
(Ⅱ)写出ξ的分布列,并求ξ的数学期望.
查看答案和解析>>
科目: 来源:湖南省四市九校2009届高三第二次联考数学试卷(理科数学) 题型:044
已知函数g(x)=-4cos2(x+![]() )+4sin(x+
)+4sin(x+![]() )-a,把函数y=g(x)的图象按向量
)-a,把函数y=g(x)的图象按向量![]() (-
(-![]() ,1)平移后得到y=f(x)的图象.
,1)平移后得到y=f(x)的图象.
(Ⅰ)求函数y=lo![]() [f(x)+8+a]的值域;
[f(x)+8+a]的值域;
(Ⅱ)当x∈[-![]() ,
,![]() ]时f(x)=0恒有解,求实数a的取值范围.
]时f(x)=0恒有解,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com