设数列{a_n}的前n项和为S_n，对一切n∈N^*，点(n，S_n)在函数f(x)＝x²＋x的图象上．

(1)求a_n的表达式；

(2)设使得不等式

都成立？若存在，求出a的取值范围；若不存在，请说明理由；

(3)将数列{a_n}依次按1项，2项循环地分为(a₁)，(a₂，a₃)，(a₄)，(a₇)，(a₈，a₉)，(a₁₀)，…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为{b_n}，求b₁₀₀的值；

(4)如果将数列{a_n}依次按1项，2项，3项，…，m(m≥3)项循环；分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为{b_n}，提出同(3)类似的问题((3)应当作为特例)，并进行研究，你能得到什么样的结论？

已知：f(x)＝log_ax(0＜a＜1)．若数列{a_n}使得2，f(a₁)，f(a₂)，…，f(a_n)，2n＋4(n∈N^*)成等差数列．

(1)求数列{a_n}的通项；

(2)设b_n＝a_nf(a_n)，若{b_n}的前n项和为S_n，求S_n．

函数是这样定义的：对于任意整数m，当实数x满足不等式时，有f(x)＝m．

(1)求函数的定义域D，并画出它在x∈D∩[0，4]上的图像；

(2)若数列，记S_n＝f(a₁)＋f(a₂)＋f(a₃)＋…＋f(a_n)，求S_n；

(3)若等比数列{b_n}的首项是b₁＝1，公比为a(q＞0)，又f(b₁)＋f(b₂)＋f(b₃)＝4求公比q的取值范围．

已知二次函数y＝f(x)对任意x∈R满足f(x－1)＝f(－x)，且图像经过点(－2，1)及坐标原点．

(1)求函数y＝f(x)的解析式；

(2)设数列{a_n}前n项和S_n＝f(n)，求数列{a_n}的通项公式a_n；

(3)对(2)中a_n，设为数列{b_n}前n项和，试问：是否存在关于n的整式g(n)，使得T₁＋T₂＋…＋T_n－1＝(T_n－1)g(n)对于一切不小于2的自然数n恒成立？若存在，写出g(n)的解析式，并加以证明；若不存在，请说明理由．

如图是一个具有n行n列的数表，第一行是首项为1，公比为q的等比数列，第一列是首项为1，公差为d的等差数列，其它空格按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写．设a_ij表示第i行第j列的数．

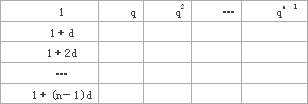
(1)求a₂₂，a₃₂及a_n2的表达式；

(2)第二行能否构成等比数列？若能，求出q，d满足的条件；若不能，请说明理由．

(3)请根据这张数表提出一个与问题(2)相类似的问题，并加以研究和解决(根据所提问题的难度及解答情况评分)．

已知数列{a_n}满足a₁＝a(a为常数，a∈R，a_n+1＝2ⁿ－3a_n(n∈N^*)，设．

(1)求数列{b_n}所满足的递推公式；

(2)求常数c、q使得b_n+1－c＝q(b_n－c)对一切n∈N^*恒成立；

(3)求数列{a_n}通项公式，并讨论：是否存在常数a，使得数列{a_n}为递增数列？若存在，求出所有这样的常数a；若不存在，说明理由．

我们规定：对于任意实数A，若存在数列{a_n}和实数x(x≠0)，使得A＝a₁＋a₂x＋a₃x²＋…＋a_nx^n－1，则称数A可以表示成x进制形式，简记为：

．如：，则表示A是一个2进制形式的数，且A＝－1＋3×2＋(－2)×2²＋1×2³＝5．

(1)已知m＝(1－2x)(1＋3x²)(其中x≠0)，试将m表示成x进制的简记形式．

(2)若数列{a_n}满足a₁＝2，，

，是否存在实常数p和q，对于任意的n∈N^*，b_n＝p·8ⁿ＋q总成立？若存在，求出p和q；若不存在，说明理由．

(3)若常数t满足t≠0且t＞－1，，求．

已知f(x)＝log₂x，若2，f(a₁)，f(a₂)，f(a_n)，2n＋4，…(n∈N^*)成等差数列．

(1)求数列{a_n}(n∈N^*)的通项公式；

(2)设g(k)是不等式整数解的个数，求g(k)；

(3)在(2)的条件下，试求一个数列{b_n}，使得．

对于给定数列{c_n}，如果存在实常数p，q使得c_n+1＝pc_n＋q对于任意n∈NN*都成立，我们称数列{c_n}是“M类数列”．

(1)若a_n＝2n，b_n＝3·2ⁿ，n∈N^*，数列{a_n}、{b_n}是否为“M类数列”？若是，指出它对应的实常数p，q，若不是，请说明理由；

(2)证明：若数列{a_n}是“M类数列”，则数列{a_n＋a_n+1}也是“M类数列”；

(3)若数列{a_n}满足a₁＝2，a_n＋a_n+1＝3t·2ⁿ(n∈N^*)，t为常数．求数列{a_n}前2009项的和．并判断{a_n}是否为“M类数列”，说明理由；

(4)根据对(2)(3)问题的研究，对数列{a_n}的相邻两项a_n、a_n+1，提出一个条件或结论与“M类数列”概念相关的真命题，并探究其逆命题的真假．

已知，数列{a_n}有a₁＝a，a₂＝p(常数p＞0)，对任意的正整数n，S_n＝a₁＋a₂＋…＋a_n，并有S_n满足．

(1)求a的值；

(2)试确定数列{a_n}是不是等差数列，若是，求出其通项公式．若不是，说明理由；

(3)对于数列{b_n}，假如存在一个常数b使得对任意的正整数n都有b_n＜b且，则称b为数列{b_n}的“上渐进值”，令，求数列{p₁＋p₂＋…＋p_n－2n}的“上渐进值”．