
科目: 来源:2009年高考数学第二轮执点专题测试:立体几何(含详解) 题型:044
如图1所示,在边长为12的正方形![]() 中,点B、C在线段
中,点B、C在线段![]() 上,且AB=3,BC=4,作BB1∥AA1,分别交A1
上,且AB=3,BC=4,作BB1∥AA1,分别交A1![]() 、A
、A![]() 于点B1、P,作CC1∥AA1,分别交A1
于点B1、P,作CC1∥AA1,分别交A1![]() 、A
、A![]() 于点C1、Q,将该正方形沿BB1、CC1折叠,使得
于点C1、Q,将该正方形沿BB1、CC1折叠,使得![]() 与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.

(Ⅰ)在三棱柱ABC-A1B1C1中,求证:AB⊥平面BCC1B1;
(Ⅱ)求平面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比.
查看答案和解析>>
科目: 来源:2009年高考数学第二轮执点专题测试:立体几何(含详解) 题型:044
在四棱锥P-ABCD中,△PBC为正三角形,AB⊥平面PBC,AB∥CD,AB=![]() DC,E为PD中点.
DC,E为PD中点.

(1)求证:AE∥平面PBC;
(2)求证:AE⊥平面PDC.
查看答案和解析>>
科目: 来源:2009年高考数学第二轮执点专题测试、平面解析几何(含详解) 题型:044
已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为![]() 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
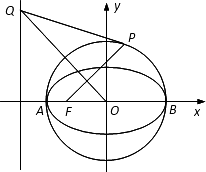
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点P的坐标为(1,1),求证:直线PQ与圆O相切;
(Ⅲ)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
查看答案和解析>>
科目: 来源:2009年高考数学第二轮执点专题测试、平面解析几何(含详解) 题型:044
已知双曲线![]() 的两个焦点为F:(-2,0),F:(2,0),点P(3,
的两个焦点为F:(-2,0),F:(2,0),点P(3,![]() )的曲线C上.
)的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为![]() 求直线l的方程
求直线l的方程
查看答案和解析>>
科目: 来源:2009年高考数学第二轮执点专题测试、平面解析几何(含详解) 题型:044
已知圆O:x2+y2=1,圆C:(x-2)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如下图,满足|PA|=|PB|.

(Ⅰ)求实数a、b间满足的等量关系;
(Ⅱ)求切线长|PA|的最小值;
(Ⅲ)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2009年高考数学第二轮执点专题测试、平面解析几何(含详解) 题型:044
若椭圆![]() 过点(-3,2),离心率为
过点(-3,2),离心率为![]() ,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为(x-8)2+(y-6)2=4,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为(x-8)2+(y-6)2=4,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
(1)求椭圆的方程;
(2)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的直线方程;
(3)求![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目: 来源:2009届上海市南汇中学高三年级零次月考、数学试卷 题型:044
在二项式定理这节教材中有这样一个性质:![]()
(1)计算![]() 的值方法如下:
的值方法如下:
设![]() 又
又![]()
相加得![]() 即2S=5·23
即2S=5·23
所以2S=5·22=20利用类似方法求值:
![]()
(2)将(1)的情况推广到一般的结论,并给予证明
(3)设Sn是首项为a1,公比为q的等比数列{an}的前n项的和,求
![]()
查看答案和解析>>
科目: 来源:2009届上海市南汇中学高三年级零次月考、数学试卷 题型:044
在平面直角坐标系xoy中,直线l与抛物线y2=2x相交于A、B两点.
(1)求证:“如果直线l过点T(3,0),那么![]() ”是真命题;
”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
查看答案和解析>>
科目: 来源:2009届上海市南汇中学高三年级零次月考、数学试卷 题型:044
一个倒立圆锥形容器,它的轴截面是正三角形,在这个容器内注入水并且放入一个半径为r的铁球,这时水面恰好和球面相切,将球从圆锥内取出后,圆锥内水平面高是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com