给定抛物线C：y²＝4x，F是C的焦点，过点F的直线l与C相交于A、B两点，记O为坐标原点．

(Ⅰ)求的值；

(Ⅱ)设，当三角形OAB的面积时，求λ的取值范围．

设a∈R，函数f(x)＝2x³－3(a＋2)x²＋12ax＋4．

(Ⅰ)若x＝3是f(x)的一个极值点，求常数a的值；

(Ⅱ)若f(x)在(－∞，1)上为增函数，求a的取值范围．

设{a_n}是公差d≠0的等差数列，S_n是其前n项的和．

(Ⅰ)若a₁＝4，且的等比中项是，求数列{a_n}的通项公式；

(Ⅱ)是否存在p，q∈N^*，且p≠q，使得S_p+q是S_2p和S_2q的等差中项？证明你的结论．

如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧面PAD是正三角形，且平面PAD⊥底面ABCD．

(Ⅰ)求证：AB⊥平面PAD；

(Ⅱ)求直线PC与底面ABCD所成角的大小；

(Ⅲ)设AB＝1，求点D到平面PBC的距离．

甲、乙两人进行一场乒乓球比赛，根据以往经验，单局比赛甲胜乙的概率为0.4．场比赛采用五局三胜制，即先胜三局的人获胜，比赛结束．设各局比赛相互间没有影响，求：

(Ⅰ)前三局比赛乙领先的概率；

(Ⅱ)本场比赛甲以3∶2取胜的概率．

△ABC中，内角A、B、C的对边分别为a、b、c，且．

(Ⅰ)求角C的大小；

(Ⅱ)若a、b、c成等比数列，求sinA的值．

已知数列{a_n}中，前n项和为S_n，点(a_n＋1，S_n+1)在直线y＝4x－2上，其中n＝1，2，3，…．

(Ⅰ)设b_n＝a_n+1－2a_n，且a₁＝1，求证数列{b_n}是等比数列；

(Ⅱ)令f(x)＝b₁x＋b₂x²＋…＋b_nxⁿ，求函数f(x)在点x＝1处的导数并比较与6n²－3n的大小．

已知双曲线的离心率为，且过点．

(Ⅰ)求双曲线C的方程；

(Ⅱ)若直线与双曲线C恒有两个不同的交点A和B，且，求k的取值范围．

经统计，某校教工食堂一个售饭窗口每天中午排队买饭的教工人数及相应的概率如下：

(Ⅰ)每天中午不超过20位教工排队买饭的概率是多少？

(Ⅱ)一周5个工作日中，若有3天或3天以上中午出现超过15位教工排队买饭的概率大于0.80，学校就需要增加售饭窗口，请问该学校是否需要增加售饭窗口？

如图，已知三棱锥P－ABC中，PA⊥平面ABC，AN⊥BC于N，D是AB的中点，且PA＝1，．

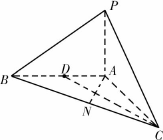
(Ⅰ)求证：PB⊥AC；

(Ⅱ)求异面直线CD与PB所成角的大小；

(Ⅲ)求点A到平面PBC的距离．