已知数列{a_n}满足：a₁＝1且a_n+1＝，n∈N^*

(Ⅰ)若数列{b_n}满足：b_n＝(n∈N^*)，试证明数列{b_n－1}是等比数列；

(Ⅱ)求数列{a_nb_n}的前n项和S_n；

(Ⅲ)数列{a_n－b_n}是否存在最大项，如果存在求出，若不存在说明理由．

如图所示，F是双曲线＝1(a＞0，b＞0)的左焦点，M是渐近线与左准线在第二象限内的一个交点．

(Ⅰ)求证：点M在以原点为圆心，a为半径的圆O上；

(Ⅱ)求证：直线FM与圆O相切；

(Ⅲ)直线FM与右准线交于N点，连ON交圆O于E点．若|NE|＝2a，且直线FM截双曲线所得弦长为2，求双曲线的方程．

(Ⅰ)若f(x)在区间[1，]内单调递增，求a的取值范围；

(Ⅱ)如果点x₀使得f(x₀)＝x₀，则称点x₀为函数y＝f(x)的一个不动点，若已知f(x)的导函数f′(x)在区间[－1，1]内恰有一个不动点，求a的取值范围．

如图，在直三棱柱ABC－A₁B₁C₁中，AC⊥BC，AA₁＝AC＝BC＝2，D、E、F分别是AB、AA₁、CC₁的中点，P是CD上的点．

(Ⅰ)求证直线PE∥平面A₁BF；

(Ⅱ)求二面角D－EC－A的大小；

(Ⅲ)求直线PE与平面A₁BF的距离．

在△ABC中，a、b、c分别是角A、B、C所对边的长，S是△ABC的面积．已知S＝a²－(b－c)²，求tanA的值．

已知F₁(－2，0)，F₂(2，0)，点P满足|PF₁|－|PF₂|＝2，记点P的轨迹为E，

(Ⅰ)求轨迹E的方程；

(Ⅱ)若直线过点F₂且与轨迹E交于P、Q两点，

①无论直线l绕点F₂怎样转动，在x轴上总存在定点M(m，0)，使MP⊥MQ恒成立，求实数m的值；

②过P、Q作直线x＝的垂线PA、QB，垂足分别为A、B，记，求λ的取值范围．

已知二次函数f(x)＝x²－ax＋a(x∈R)同时满足：(1)不等式f(x)≤0的解集有且只有一个元素；(2)在定义域内存在0≤x₁＜x₂，使得不等式f(x₁)＞f(x₂)成立．设数列{a_n}的前n项和S_n＝f(n)．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)设b_n＝，求数列{b_n}的前n项和；

(Ⅲ)设各项均不为零的数列{c_n}中，所有满足c_i·c_i+1＜0的正整数i的个数称为这个数列{c_n}的变号数．另(n为正整数)，求数列{c_n}的变号数．

定义在R上的函数f(x)＝x³＋ax²＋bx(a，b)为常数在x＝－1处取得极值，且f(x)的图象在P(1，f(1))处的切线平行与直线y＝8x．

(Ⅰ)求函数f(x)的解析式及极值；

(Ⅱ)设k＞0，求不等式f(x)≥kx的解集；

(Ⅲ)对任意α，β∈R，求证：|f(sinα)－f(cosβ)≤．

在直三棱柱ABC－A₁B₁C₁中，∠ACB＝90°，BC＝CC₁＝a，AC＝2a．

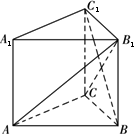
(Ⅰ)求证：AB₁⊥BC₁；

(Ⅱ)求二面角B－AB₁－C的大小；

(Ⅲ)求点A₁到平面AB₁C的距离．

把圆周分成四等份，A是其中一个分点，动点P在四个分点上按逆时针方向前进．现在投掷一个质地均匀的正四面体，它的四个面上分别写有1，2，3，4四个数字．P从A点出发，按照正四面体底面上数字前进几个分点，转一周之前连续投掷．

(Ⅰ)求点P恰好返回A点的概率；

(Ⅱ)在点P转一周恰能返回A点的所有结果中，用随机变量ξ表示点P能返回A点的投掷次数，求ξ的分数列和期望．