已知△ABC中，a、b、c分别是角A、B、C的对边，且．

(Ⅰ)求角B的大小；

(Ⅱ)设b＝，a＋c＝4，求A．

如图，直角梯形ABCD中，∠DAB＝90°，AD∥BC，AB＝2，，，椭圆F以A、B为焦点且过点D．

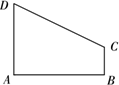
(Ⅰ)建立适当的直角坐标系，求椭圆的方程；

(Ⅱ)若点E满足，是否存在斜率k≠0的直线l与椭圆交于M、N两点，且|ME|＝|NE|，若存在，求k的取值范围；若不存在，说明理由．

已知函数f(x)＝ax³＋bx²－3x在x＝±1处取得极值．

(Ⅰ)求函数f(x)的解析式；

(Ⅱ)若过点A(1，m)(m≠－2)可作曲线y＝f(x)的三条切线，求实数m的取值范围．

如图，正三棱柱ABC－A₁B₁C₁的底面边长为a，点M在边BC上，△AMC₁是以点M为直角顶点的等腰直角三角形．

(Ⅰ)求证点M为边BC的中点；

(Ⅱ)求点C到平面AMC₁的距离；

(Ⅲ)求二面角M－AC₁－C的大小．

对于函数f(x)，若存在x₀∈R，使f(x₀)＝x₀成立，则称x₀为f(x)的“滞点”．已知函数．

(Ⅰ)试问f(x)有无“滞点”？若有求之，否则说明理由；

(Ⅱ)已知数列{a_n}的各项均为负数，且满足，求数列{a_n}的通项公式；

(Ⅲ)已知b_n＝a_n·2ⁿ，求{b_n}的前n项和T_n．

在2006年多哈亚运会中，中国女排与日本女排以“五局三胜”制进行决赛，根据以往战况，中国女排每一局赢的概率为．已知比赛中，第一局日本女排先胜一局，在这个条件下，

(Ⅰ)求中国女排取胜的概率；

(Ⅱ)求决赛中共进行4场比赛的概率．

(Ⅰ)(Ⅱ)均用分数作答)

已知向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，．

(Ⅰ)求cos(α－β)的值；

(Ⅱ)若，且，求sinα的值．

设．

(Ⅰ)若f(x)在区间内单调递增，求a的取值范围；

(Ⅱ)如果点x₀使得f(x₀)＝x₀，则称点x₀为函数y＝f(x)的一个不动点，若已知f(x)的导函数在区间[－1，1]内恰有一个不动点，求a的取值范围．

如图所示，F是双曲线(a＞0，b＞0)的左焦点，M是渐近线与左准线在第二象限内的一个交点．

(Ⅰ)求证：点M在以原点为圆心，a为半径的圆O上；

(Ⅱ)求证：直线FM与圆O相切；

(Ⅲ)直线FM与右准线交于N点，连ON交圆O于E点．若|NE|＝2a，且直线FM截双曲线所得弦长为．求双曲线的方程．

已知S_n是等比数列{a_n}的前n项和，a₁＝1，S₁、S₃、S₂成等差数列．

(Ⅰ)求数列{a_n}的通项；

(Ⅱ){b_n}为等差数列，且b₁＝S₁、b₂＝S₃、b₃＝S₂，求数列{a_nb_n}的前n项和T_n．