某工厂有工人1 000名，其中250名工人参加过短期培训(称为A类工人)，另外750名工人参加过长期培训(称为B类工人)，现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人，调查他们的生产能力(此处生产能力指一天加工的零件数)．

(Ⅰ)A类工人中和B类工人各抽查多少工人？

(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2

表1：

表2：

(i)先确定x，y，再在答题纸上完成下列频率分布直方图．就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？(不用计算，可通过观察直方图直接回答结论)

(ii)分别估计A类工人和B类工人生产能力的平均数，并估计该工厂工人的生产能力的平均数，同一组中的数据用该组区间的中点值作代表)

如下图，在三棱锥P－ABC中，△PAB是等边三角形，∠PAC＝∠PBC＝90°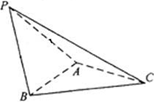

(Ⅰ)证明：AB⊥PC

(Ⅱ)若PC＝4，且平面PAC⊥平面PBC，求三棱锥P－ABC体积．

如图，为了解某海域海底构造，在海平面内一条直线上的A，B，C三点进行测量，已知AB＝50 m，BC＝120 m，于A处测得水深AD＝80 m，于B处测得水深BE＝200 m，于C处测得水深CF＝110 m，求∠DEF的余弦值．

选修4－5：不等式选讲

如图，O为数轴的原点，A，B，M为数轴上三点，C为线段OM上的动点，设x表示C与原点的距离，y表示C到A距离4倍与C道B距离的6倍的和．

(1)将y表示成x的函数；

(2)要使y的值不超过70，x应该在什么范围内取值？

选修4－4：坐标系与参数方程．

已知曲线C：(t为参数)，C₂：(为参数)．

(1)化C₁，C₂的方程为普通方程，并说明它们分别表示什么曲线；

(2)若C₁上的点P对应的参数为t＝，Q为C₂上的动点，求PQ中点M到直线

C₃：(t为参数)距离的最小值．

选修4－1：几何证明选讲

如图，已知△ABC的两条角平分线AD和CE相交于H，∠B＝60°，F在AC上，且AE＝AF．

(Ⅰ)证明：B，D，H，E四点共圆：

(Ⅱ)证明：CE平分∠DEF．

已知函数f(x)＝(x³＋3x²＋ax＋b)e^－x

(Ⅰ)如a＝b＝－3，求f(x)的单调区间；

(Ⅱ)若f(x)在(－∞，α)，(2，α)单调增加，在(α，2)，(β，＋∞)单调减少，证明β－α＜6．

已知椭圆C的中心为直角坐标系xOy的原点，焦点在s轴上，它的一个顶点到两个焦点的距离分别是7和1．

(Ⅰ)求椭圆C的方程；

(Ⅱ)若P为椭圆C上的动点，M为过P且垂直于x轴的直线上的点，＝λ，求点M的轨迹方程，并说明轨迹是什么曲线．

如图，四棱锥S－ABCD的底面是正方形，每条侧棱的长都是地面边长的倍，P为侧棱SD上的点．

(Ⅰ)求证：AC⊥SD；

(Ⅱ)若SD⊥平面PAC，求二面角P－AC－D的大小(Ⅲ)在(Ⅱ)的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC．若存在，求SE：EC的值；若不存在，试说明理由．

某工厂有工人1 000名，其中250名工人参加过短期培训(称为A类工人)，另外750名工人参加过长期培训(称为B类工人)，现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人，调查他们的生产能力(此处生产能力指一天加工的零件数)．

(Ⅰ)求甲、乙两工人都被抽到的概率，其中甲为A类工人，乙为B类工人；

(Ⅱ)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2．

　　表1：

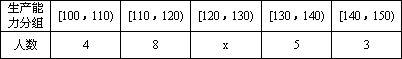
　　表2：

(ⅰ)先确定x，y，再在答题纸上完成下列频率分布直方图．就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？(不用计算，可通过观察直方图直接回答结论)

(ⅱ)分别估计A类工人和B类工人生产能力的平均数，并估计该工厂工人的生产能力的平均数，同一组中的数据用该组区间的中点值作代表)