如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝PA＝a，点O、D分别是AC、PC的中点，OP⊥底面ABC．

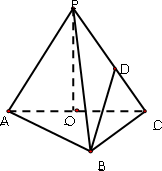
(1)求三棱锥P－ABC的体积．

(2)求异面直线PA与BD所成角余弦值的大小．

在区间(0，1)中随机地取出两个数，求两数之和小于的概率．

在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图(如图)，已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12，请解答下列问题：

(1)本次活动共有多少件作品参加评比？

(2)哪组上交的作品数量最多？共有多少件？

(3)经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪组获奖率高？

设函数f(x)＝x³＋bx²＋cx(x∈R)，已知g(x)＝f(x)－(x)是奇函数．

(1)求b、c的值．

(2)求g(x)的单调区间与极值．

已知数列{a_n}满足：a₁＝1，a_n＋1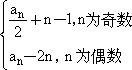＝，记b_n＝a_2n(n∈N*)，S_n为数列{b_n}的前n项和．

(Ⅰ)证明数列{b_n}为等比数列，并求其通项公式；

(Ⅱ)若对任意n∈N*且n≥2，不等式λ≥1＋S_n－1恒成立，求实数λ的取值范围；

(Ⅲ)令c_n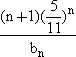＝，证明：c_n≤(n∈N*)．

已知两圆O₁：(x＋1)²＋y²＝和O₂：(x－1)²＋y²＝，动圆P与⊙O₁外切，且与⊙O₂内切．

(Ⅰ)求动圆圆心P的轨迹方程；

(Ⅱ)过点M(5，0)作直线l与点P的轨迹交于不同两点A、B，试推断是否存在直线l，使得线段AB的垂直平分线经过圆心O₂？若存在，求出直线l的方程；若不存在，说明理由．

据调查，湖南某地区有100万从事传统农业的农民，人均年收入3 000元．为了增加农民的收入，当地政府积极引资建立各种加工企业，对当地的农产品进行深加工，同时吸收当地部分农民进入加工企业工作．据估计，如果有x(x＞0)万人进入企业工作，那么剩下从事传统农业的农民的人均年收入有望提高2x％，而进入企业工作的农民人均年收入为3 000a元(a＞0为常数)．

(Ⅰ)在建立加工企业后，要使该地区从事传统农业的农民的年总收入不低于加工企业建立前的年总收入，求x的取值范围；

(Ⅱ)在(Ⅰ)的条件下，当地政府应安排多少万农民进入加工企业工作，才能使这100万农民的人均年收入达到最大？

如图，四边形ABCD是菱形，PA⊥平面ABCD，M为PA的中点．

(Ⅰ)求证：PC∥平面BDM；

(Ⅱ)若PA＝AC＝，BD＝，求直线BM与

平面PAC所成的角．

已知函数f(x)＝x³－(a－1)x²＋b²x，其中a，b为实常数．

(Ⅰ)求函数f(x)为奇函数的充要条件；

(Ⅱ)若任取a∈[0，4]，b∈[0，3]，求函数f(x)在R上是增函数的概率．

已知函数f(x)＝sin²ωx＋cosωx·cos(－ωx)(ω＞0)，且函数y＝f(x)的图象相邻两条对称轴之间的距离为．

(Ⅰ)求f()的值；

(Ⅱ)若函数f(kx＋)(k＞0)在区间[－，]上单调递增，求k的取值范围．