如图所示，已知PA与⊙O相切，A为切点，PBC为割线，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且∠EDF＝∠ECD．

(1)求证：EF·EP＝DE·EA；

(2)若EB＝DE＝6，EF＝4，求PA的长．

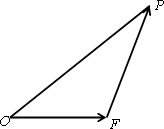
如图，设△OFP的面积为S，已知＝1．

(1)若＜S＜，求向量与的夹角的取值范围；

(2)若S＝，且≥2，当取最小值时，建立适当的直角坐标系，求以O为中心，F为一个焦点且经过点P的椭圆方程．

对于函数f(x)，若存在x₀∈R，使f(x₀)＝x₀成立，则称x₀为f(x)的不动点．如果函数f(x)＝(b，c∈N)有且只有两个不动点0，2，且f(－2)＜－．

(1)求函数f(x)的解析式；

(2)已知各项不为零的数列{a_n}满足4S_n·f()＝1(S_n为数列前n项和)，求数列通项a_n；

(3)如果数列{a_n}满足a₁＝4，a_n+1＝f(a_n)，求证：当n≥2时，恒有a_n＜3成立．

已知a为实数，f(x)＝(x²－4)(x－a)．

(1)求导数(x)；

(2)若(－1)＝0，求f(x)在[－2，2]上的最大值和最小值；

(3)若f(x)在(－∞，－2]和[2，＋∞)上都是递增的，求a的取值范围．

已知过点A(0，1)的直线l，斜率为k，与圆C：(x－2)²＋(y－3)²＝1相交于M、N两个不同点

(1)求实数k取值范围；

(2)若O为坐标原点，且＝12，求k的值．

已知A、B是△ABC的两个内角，，其中、为互相垂直的单位向量，若||＝．求tanA·tanB的值．

已知函数y＝|x|＋1，y＝，y＝(x＋)，(x＞0)的最小值恰好是方程：x³＋ax²＋bx＋c＝0的三个根，其中0＜t＜1．

(1)求证：a²＝2b＋3；

(2)设(x₁，M)、(x₂，N)是函数f(x)＝x³＋ax²＋bx＋c的两个极值点．

①若|x₁－x₂|＝，求函数f(x)的解析式；

②求|M－N|的取值范围．

已知函数y＝f(x)(x∈R)满足f(x)＋f(1－x)＝．

(1)若数列a_n满足a_n＝f(0)＋f()＋f()＋…＋f()＋f(1)，求数列{a_n}(n∈N*)的通项公式；

(2)若数列{b_n}满足a_nb_n＝，S_n＝b₁b₂＋b₂b₃＋b₃b₄＋…＋b_nb_n+1，则实数k为何值时，不等式2kS_n＜b_n恒成立．

已知a∈R，函数f(x)＝－x³＋ax²＋2ax．

(Ⅰ)当a＝1时，求函数f(x)的单调递增区间；

(Ⅱ)若函数f(x)在R上单调递减，求a的取值范围；

(Ⅲ)若函数f(x)在[－1，1]上单调递增，求a的取值范围．

在△ABC中，tanAtanB－tanA－tanB＝．

(Ⅰ)求∠C的大小；

(Ⅱ)设角A，B，C的对边依次为a，b，c，若c＝2，且△ABC是锐角三角形，求a²＋b²的取值范围．