从数列{a_n}中取出部分项，并将它们按原来的顺序组成一个数列，称之为数列{a_n}的一个子数列．

设数列{a_n}是一个首项为a₁、公差为d(d≠0)的无穷等差数列．

(1)若a₁，a₂，a₅成等比数列，求其公比q．

(2)若a₁＝7d，从数列{a_n}中取出第2项、第6项作为一个等比数列的第1项、第2项，试问该数列是否为{a_n}的无穷等比子数列，请说明理由．

(3)若a₁＝1，从数列{a_n}中取出第1项、第m(m≥2)项(设a_m＝t)作为一个等比数列的第1项、第2项，试问当且仅当t为何值时，该数列为{a_n}的无穷等比子数列，请说明理由．

已知椭圆C：(a＞b＞0)，其焦距为2c，若(≈0.618)，则称椭圆C为“黄金椭圆”．

(1)求证：在黄金椭圆C：(a＞b＞0)中，a、b、c成等比数列．

(2)黄金椭圆C：(a＞b＞0)的右焦点为F₂(c，0)，P为椭圆C上的

任意一点．是否存在过点F₂、P的直线l，使l与y轴的交点R满足？若存在，求直线l的斜率k；若不存在，请说明理由．

(3)在黄金椭圆中有真命题：已知黄金椭圆C：(a＞b＞0)的左、右焦点分别是F₁(－c，0)、F₂(c，0)，以A(－a，0)、B(a，0)、D(0，－b)、E(0，b)为顶点的菱形ADBE的内切圆过焦点F₁、F₂．

试写出“黄金双曲线”的定义；对于上述命题，在黄金双曲线中写出相关的真命题，并加以证明．

如图，反比例函数y＝f(x)(x＞0)的图像过点A(1，4)和B(4，1)，点P(x，y)为该函数图像上一动点，过P分别作x轴、y轴的垂线，垂足为C、D．记四边形OCPD(O为坐标原点)与三角形OAB的公共部分面积为S．

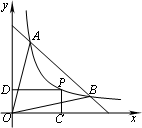
(1)求S关于x的表达式；

(2)求S的最大值及此时x的值．

在长方体ABCD－A₁B₁C₁D₁中，AB＝BC＝2，过A₁、C₁、B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD－A₁C₁D₁，且这个几何体的体积为10．

(1)求棱A₁A的长；

(2)求点D到平面A₁BC₁的距离．

已知关于x的实系数一元二次方程ax²＋bx＋c＝0有两个虚根x₁，x₂，且(1－3ai)i＝c－(i为虚数单位)，|x₁－x₂|＝1，求实数b的值．

已知：正数数列{a_n}的通项公式(n∈N^*)．

(1)求数列{a_n}的最大项；

(2)设，确定实常数p，使得{b_n}为等比数列；

(3)(理)数列{C_n}，满足C₁＞－1，C₁≠，，其中p为第(2)小题中确定的正常数，求证：对任意n∈N*，有且或且成立．

(文)设{b_n}是满足第(2)小题的等比数列，求使不等式－b₁＋b₂－b₃＋…＋(－1)ⁿb_n≥2010成立的最小正整数n．

如图，F是抛物线y²＝2px(p＞0)的焦点，Q是准线与x轴的交点，斜率为k的直线l经过点Q．

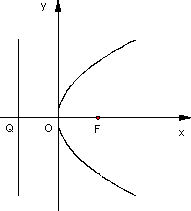
(1)当K取不同数值时，求直线l与抛物线交点的个数；

(2)如直线l与抛物线相交于A、B两点，求证：K_FA＋K_FB是定值．

(3)在x轴上是否存在这样的定点M，对任意的过点Q的直线l，如l与抛物线相交于A、B两点，均能使得k_MA·k_MB为定值，有则找出满足条件的点M；没有，则说明理由．

如图所示，某人在斜坡P处仰视正对面山顶上一座铁塔，塔高AB＝80米，塔所在山高OA＝220米，OC＝200米，观测者所在斜坡CD近似看成直线，斜坡与水平面夹角为α，

(1)以射线OC为Ox轴的正向，OB为Oy轴正向，建立直角坐标系，求出斜坡CD所在直线方程；

(2)当观察者P视角∠APB最大时，求点P的坐标(人的身高忽略不计)．

△ABC中，角A、B、C的对边依次为a、b、c．已知a＝3，b＝4，外接圆半径，c边长为整数．

(1)求∠A的大小(用反三角函数表示)；

(2)求边长c；

(3)在AB、AC上分别有点D、E，线段DE将△ABC分成面积相等的两部分，求线段DE长的最小值．

如图，四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA＝AB＝1，BC＝2，E为PD的中点．

(1)求异面直线PA与CE所成角的大小；

(2)求二面角E－AC－D的大小．

求三棱锥A－CDE的体积．