已知函数f(x)＝3ax⁴－2(3a＋2)x²＋4x．

(Ⅰ)当a＝时，求f(x)的极值；

(Ⅱ)若f(x)在(－1，1)上是增函数，求a的取值范围．

如图，四棱锥S－ABCD中，SD⊥底面ABCD，AB∥DC，AD⊥DC，AB＝AD＝1，DC＝SD＝2，E为棱SB上的一点，平面EDC⊥平面SBC．

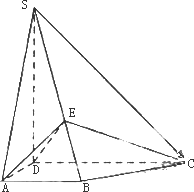
(Ⅰ)证明：SE＝2EB；

(Ⅱ)求二面角A－DC－C的大小．

投到某杂志的稿件，先由两位初审专家进行评审，若能通过两位初审专家的评审，则予以录用：若两位初审专家都未予通过，则不予录用：若恰能通过一位初审专家的评审，则再由第三位专家进行复审，若能通过复审专家的评审，则予以录用，否则不予录用．设稿件能通过各初审专家评审的概率均为0.5，复审的稿件能通过评审的概率为0.3．各专家独立评审．

(Ⅰ)求投到该杂志的1篇稿件被录用的概率；

(Ⅱ)求投到该杂志的4篇稿件中，至少有2篇被录用的概率．

已知△ABC的内角A，B及其对边a，b满足a＋b＝acotA＋bcotB，求内角C．

记等差数列{a_n}的前n项和为S，设S_x＝12，且2a₁，a₂，a₃＋1成等比数列，求S_n．

某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇．

(Ⅰ)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇，试确定小艇航行速度的最小值；

(Ⅲ)是否存在v，使得小艇以v海里/小时的航行速度行驶，总能有两种不同的航行方向与轮船相遇？若存在，试确定v的取值范围；若不存在，请说明理由．

如图，在长方体ABCD–A₁B₁C₁D₁中，E，H分别是棱A₁B₁，D₁C₁上的点(点E与B₁不重合)，且EH∥A₁D₁．过EH的平面与棱BB₁，CC₁相交，交点分别为F，G．

(Ⅰ)证明：AD∥平面EFGH；

(Ⅱ)设AB＝2AA₁＝2a．在长方体ABCD－A₁B₁C₁D₁内随机选取一点，记该点取自于几何体A₁ABFE–D₁DCGH内的概率为p．当点E，F分别在棱A₁B₁，B₁B上运动且满足EF＝a时，求p的最小值．

已知抛物线C：y²＝2px(p＞0)过点A(1，－2)．

(Ⅰ)求抛物线C的方程，并求其准线方程；

(Ⅱ)是否存在平行于OA(O为坐标原点)的直线L，使得直线L与抛物线C有公共点，且直线OA与L的距离等于？若存在，求直线L的方程；若不存在，说明理由．

设平顶向量a_m＝(m，1)，b_n＝(2，n)，其中m，n∈{1，2，3，4}．

(Ⅰ)请列出有序数组(m，n)的所有可能结果；

(Ⅱ)记“使得a_m⊥(a_m－b_n)成立的(m，n)”为事件A，求事件A发生的概率．

数列{a_n}中a＝，前n项和S_n满足S_n+1－S_n＝(n∈N^*)．

(Ⅰ)求数列{a_n}的通项公式a_n以及前n项和S_n；

(Ⅱ)若S₁，t(S₁＋S₂)，3(S₂＋S₃)成等差数列，求实数t的值．