如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，D，E分别为AB，CD的中点，AE的延长线交CB于F．现将△ACD沿CD折起，折成二面角A－CD－B，连接AF．

(Ⅰ)求证：平面AEF⊥平面CBD；

(Ⅱ)当AC⊥BD时，求二面角A－CD－B大小的余弦值．

在一个盒子中有n＋2(n≥2，n∈N^*)个球，其中2个球的标号是不同的偶数，其余n个球的标号是不同的奇数．甲乙两人同时从盒子中各取出2个球，若这4个球的标号之和为奇数，则甲胜；若这4个球的标号之和为偶数，则乙胜．规定：胜者得2分，负者得0分．

(Ⅰ)当n＝3时，求甲的得分ξ的分布列和期望；

(Ⅱ)当乙胜概率为时，求n的值．

在△ABC中，角A，B，C所对的边分别为a，b，c，且满足sinB＋cosB＝，a＝1．

(Ⅰ)求角B的大小；

(Ⅱ)若b是a和c的等比中项，求△ABC的面积．

选修4－4：坐标系与参数方程

在直角坐标系xoy中，直线l的参数方程为(t为参数)．在极坐标系(与直角坐标系xoy取相同的长度单位，且以原点o为极点，以x轴正半轴为极轴)中，圆c的方程为p＝2sin．

(Ⅰ)求圆c的直角坐标方程；

(Ⅱ)设圆c与直线l交于点A，B．若点P的坐标为(3，)，求|PA|＋|PB|．

(1)已知函数f(x)＝x³＝x，其图像记为曲线C．

(i)求函数f(x)的单调区间；

(ii)证明：若对于任意非零实数x₁，曲线C与其在点P₁(x₁，f(x₁)处的切线交于另一点P₂(x₂，f(x₂)曲线C与其在点P₂处的切线交于另一点P₃(x₃f(x₃))，线段P1P2，P2P3与曲线C所围成封闭图形的面积分别记为S1，S2，则为定值：

(Ⅱ)对于一般的三次函数g(x)＝ax³＋bx²＋cx＋d(a≠0)，请给出类似于(Ⅰ)(ii)的正确命题，并予以证明．

某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以u海里/小时的航行速度匀速行驶，经过t小时与轮船相遇．

(Ⅰ)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．

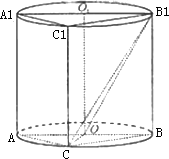
如图，圆柱OO₁内有一个三棱柱ABC－A₁B₁C₁，三棱柱的底面为圆柱底面的内接三角形，且AB是圆O的直径．

(Ⅰ)证明：平面A₁ACC₁⊥平面B₁BCC₁；

(Ⅱ)设AB＝AA₁，在圆柱OO₁内随机选取一点，记该点取自三棱柱ABC－A₁B₁C₁内的概率为p．

(i)当点C在圆周上运动时，求p的最大值；

(ii)圭亚那平面A₁ACC₁与平面B₁OC所成的角为(0°≤90°)．当p取最大值时，求cos的值．

已知在坐标原点O的椭圆C经过点A(2，3)，且点F(2，0)为其右焦点．

(Ⅰ)求椭圆C的方程；

(Ⅱ)是否存在平行于OA的直线L，使得直线L与椭圆C有公共点，且直线OA与L的距离等于4？若存在，求出直线L的方程；若不存在，说明理由．

设S是不等式x²－x－6≤0的解集，m，n∈S．

(Ⅰ)记“使得m＋n＝0成立的有序数组(m，n)”为事件A，试列举A包含的基本事件；

(Ⅱ)设ξ＝m²，求ξ的分布列及其数学期望Eξ．

已知函数f(x)＝，g(x)＝alnx，a∈R．

(1)若曲线y＝f(x)与曲线y＝g(x)相交，且在交点处有相同的切线，求a的值及该切线的方程；

(2)设函数h(x)＝f(x)－g(x)，当h(x)存在最小之时，求其最小值(a)的解析式；

(3)对(2)中的(a)，证明：当a∈(0，＋∞)时，(a)≤1．