已知函数f(x)＝sinx，数列{a_n}满足a_n＝，a_n+1＝f(a_n)．

(1)求证：当x∈(0，)时，不等式x＜f(x)＜x恒成立；

(2)设S_n为数列{a_n}的前n项和，求证：≤S_n≤[()ⁿ－1]．

已知椭圆C：(a＞b＞0)经过点P(1，)，且两焦点与短轴的一个端点构成等腰直角三角形．

(1)求椭圆的方程；

(2)动直线l：mx＋ny＋n＝0(m，n∈R)交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得以AB为直径的圆恒过点T．若存在，求出点T的坐标；若不存在，请说明理由．

如图1所示，在边长为12的正方形中，BB₁∥CC₁∥AA₁，且AB＝3，BC＝4，分别交BB₁，CC₁于点P、Q，将该正方形沿BB₁、CC₁折叠，使得与AA₁重合，构成如图2所示的三棱柱ABC－A₁B₁C₁，请在图2中解决下列问题：

(1)求证：AB⊥PQ；

(2)在底边AC上有一点M，满足AM∶MC＝3∶4，求证：BM∥平面APQ．

(3)求直线BC与平面APQ所成角的正弦值．

一个口袋中有2个白球和n个红球(n≥2，且n∈N^*)，每次从袋中摸出两个球(每次摸球后把这两个球放回袋中)，若摸出的两个球颜色相同为中奖，否则为不中奖．

(1)试用含n的代数式表示一次摸球中奖的概率P；

(2)若n＝3，求三次摸球恰有一次中奖的概率；

(3)记三次摸球恰有一次中奖的概率为f(p)，当n为何值时，f(p)最大．

在△ABC中，角A、B、C的对边分别为a，b，c，已知a＋b＝5，c＝，且4sin²－cos2C＝．

(1)求角C的大小；

(2)求△ABC的面积．

已知双曲线C的中心在坐标原点，渐近线方程是3x±2y＝0，左焦点的坐标为(－，0)，A、B为双曲线C上的两个动点，满足．

(1)求双曲线C的方程；

(2)求的值；

(3)动点P在线段AB上，满足，求证：点P在定圆上．

对于正项数列{a_n}，定义其调和平均值为A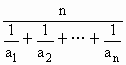(n)＝n∈N^*

(1)若A(n)＝，求{a_n}的通项公式；

(2)已知{b_n}为等比数列，且b₁＝1，公比为，其调和均值为B(n)，是否存在正整数n满足B(n)＝，如果存在，求n的值，如不存在，说明理由．

已知函数f(x)＝x³－ax²－a²x＋1，g(x)＝1－4x－ax²，其中实数a≠0，

(Ⅰ)求函数f(x)的单调区间；

(Ⅱ)若a＞0，且f(x)与g(x)在区间(－a，－a＋2)内均为增函数，求a的取值范围．

如图，四棱锥P－ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB＝60°，AB＝AD＝2CD＝2a，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD＝90°，M为AP的中点．

(1)求证：AD⊥PB；

(2)求二面角A－BC－P的正切值．

(3)求点M到平面PBD的距离．

甲，乙，丙三个同学同时报名参加某重点高校2010年自主招生，高考前自主招生的程序为审核材料和文化测试，只有审核过关才能参加文化测试，文化测试合格者即可获得自主招生入选资格，因为甲，乙，丙三人各有优势，甲，乙，丙三人审核过关的概率分别为0.5，0.6，0.4，审核过关后，甲，乙，丙三人文化测试合格的概率分别为0.6，0.5，0.75．

(1)求甲，乙，丙三人中只有一人通过审核的概率；

(2)求甲，乙，丙三人中至少有两人获得自主招生入选资格的概率．