如图，由M到N的电路中有4个元件，分别标为T₁，T₂，T₃，T₄，电流能通过T₁，T₂，T₃的概率都是p，电流能通过T₄的概率是0.9．电流能否通过各元件相互独立．已知T₁，T₂，T₃中至少有一个能通过电流的概率为0.999．

(Ⅰ)求p；

(Ⅱ)求电流能在M与N之间通过的概率；

(Ⅲ)ξ表示T₁，T₂，T₃，T₄中能通过电流的元件个数，求ξ的期望．

如图，直三棱柱ABC－A₁B₁C₁中，AC＝BC，AA₁＝AB，D为BB₁的中点，E为AB₁上的一点，AE＝3EB₁．

(Ⅰ)证明：DE为异面直线AB₁与CD的公垂线；

(Ⅱ)设异面直线AB₁与CD的夹角为45°，求二面角A₁－AC₁－B₁的大小．

已知数列{a_n}的前n项和S_n＝(n²＋n)·3ⁿ．

(Ⅰ)求；

(Ⅱ)证明：．

△ABC中，D为边BC上的一点，BD＝33，sinB＝，cos∠ADC＝，求AD．

过抛物线y²＝2px(p＞0)的对称轴上的定点M(m，0)(m＞0)，作直线AB与抛物线相交于A、B两点．

(Ⅰ)试证明A、B两点的纵坐标之积为定值；

(Ⅱ)若点N(－m，2m)，求直线AN、BN的斜率之和．

已知数列{a_n}的前n项和为S_n，且满足a₁＝1，tS_n－(2t＋1)S_n－1＝t，其中t＞0，n∈N﹡，n≥2．

(Ⅰ)求证：数列{a_n}是等比数列；

(Ⅱ)设数列{a_n}的公比为f(t)数列{b_n}满足b₁＝1，b_n＝f()(n≥2)，求数列{b_n}的通项公式；

(Ⅲ)在(Ⅱ)的条件下，若t＝1，数列{b_n}的前n项和为T_n，试比较a_n和T_n的大小关系．

定义在R上的函数f(x)＝ax³＋bx²＋cx＋d满足：函数f(x)的图象关于原点对称且过点(3，－6)，函数f(x)在点x₁、x₂处取得极值，且|x₁－x₂|＝4．

(Ⅰ)求函数f(x)的表达式；

(Ⅱ)求函数f(x)的单调区间；

(Ⅲ)求函数f(x)过点P(1，－8)的切线方程．

已知斜三棱柱ABC－A₁B₁C₁的侧面A₁ACC₁与底面ABC垂直，∠ABC＝90°，BC＝2，AC＝2，且AC＝AA₁＝A₁C

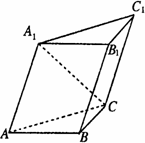
(Ⅰ)求侧棱AA₁与底面ABC所成角的大小；

(Ⅱ)求侧面A₁ABB₁与底面ABC所成二面角的正切值；

(Ⅲ)求侧棱B₁B和侧面A₁ACC₁的距离．

某种项目的射击比赛，开始时在距目标100 m射击，如果命中记6分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已经在150 m处，这时命中记3分，且停止射击；若第二次仍未命中，还可以进行第三次射击，此时目标已经在200 m处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分，且不再继续射击．已知射手甲在100 m处击中目标的概率为，他的命中率与其距目标距离的平方成反比，且各次射击是否击中目标是相互独立的．

(Ⅰ)分别求这名射手在150 m处、200 m处的命中率；

(Ⅱ)求这名射手停止射击时已击中目标的概率．

已知函数f(x)＝Asin(ωx＋)＋B(A＞0，ω＞0，0≤＜2π)在同一周期内有最高点(，1)和最低点(，－3)．

(Ⅰ)求函数y＝f(x)的解析式；

(Ⅱ)画出函数y＝f(x)在区间[0，π]上的图象．