给出下面的数表序列：

其中表n(n＝1，2，3…)有n行，第1行的n个数是1，3，5，…2n－1，从第2行起，每行中的每个数都等于它肩上的两数之和．

(Ⅰ)写出表4，验证表4各行中数的平均数按从上到下的顺序构成等比数列，并将结论推广到表n(n≥3)(不要求证明)；

(Ⅱ)每个数列中最后一行都只有一个数，它们构成数列1，4，12…，记此数列为{b_n}求和：(n∈N^*)．

为了考察冰川的融化状况，一支科考队在某冰川山上相距8 Km的A、B两点各建一个考察基地，视冰川面为平面形，以过A、B两点的直线为x轴，线段AB的垂直平分线为y轴建立平面直角坐标系(下图)．考察范围到A、B两点的距离之和不超过10 Km的区域．

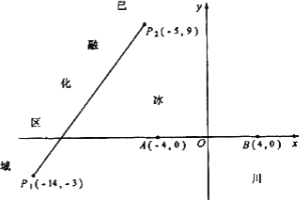
(Ⅰ)求考察区域边界曲线的方程：

(Ⅱ)如图所示，设线段P₁P₂是冰川的部分边界线(不考虑其他边界)，当冰川融化时，边界线沿与其垂直的方向朝考察区域平行移动，第一年移动0.2 km，以后每年移动的距离为前一年的2倍．问：经过多长时间，点A恰好在冰川边界线上？

如图所示，在长方体ABCD－A₁B₁C₁D₁中，AB＝AD＝1，AA₁＝2，M是棱CC₁的中点

(Ⅰ)求异面直线A₁M和C₁D₁所成的角的正切值；

(Ⅱ)证明：平面ABM⊥平面A₁B₁M₁

为了对某课题进行研究，用分层抽样方法从三所高校A，B，C的相关人员中，抽取若干人组成研究小组、有关数据见下表(单位：人)

(Ⅰ)求x，y；

(Ⅱ)若从高校B、C抽取的人中选2人作专题发言，求这二人都来自高校C的概率．

已知a是给定的实常数，设函数f(x)＝(x－a²)(x＋b)e^X，b∈R，x＝a是f(x)的一个极大值点．

(1)求b的取值范围；

(2)设x₁，x₂，x₃是f(x)的3个极致点，问是否存在实数b，可找到x₄∈R，使得x₁，x₂，x₃，x₄的某种排列x_i1，x_i2，x_i3，x_i4(其中{i₁，i_2，I_3，i₄}＝{1，2，3，4})依次成等差数列？若存在，求所有的b及相应的x₄；若不存在，说明理由．

已知m＞1，直线l：x－my－²＝0，椭圆C：()²＋y²＝4，F₁，F₂分别为椭圆C的左右焦点．

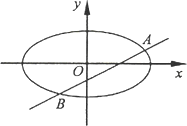
(Ⅰ)当直线l过右焦点F₂时，求直线l的方程；

(Ⅱ)设直线l与椭圆C交与A，B两点，△AF₁F₂．△BF₁F₂的重心分别为G，H.若原点O在以线段GH为直径的的圆内，求实数m的取值范围．

如图，在矩形ABCD中，点E，F分别在线段AB，AD上，AE＝EB＝AF＝FD＝4．沿直线EF将△AEF翻着成△EF，使平面EF⊥平面BEF．

(Ⅰ)求二面角－FD－C的余弦值；

(Ⅱ)点M，N分别在线段FD，BC上，若沿直线MN将四边形MNCD向上翻着，使C与重合，求线段FM的长．

如图，一个小球从M处投入，通过管道自上而下落到A或B或C．已知小球从每个叉口落入左右两个管道的可能性是相等的．

某商家按上述投球方式进行促销活动，若投入的小球落到A，B，C，则分别设为1，2，3等奖．

(Ⅰ)已知获得1，2，3等奖的折扣率分别为50％，70％，90％．记随机变量ξ为获得k(k＝1，2，3)等奖的折扣率，求随机变量ξ的分布列及期望Eξ；

(Ⅱ)若有3人次(投入1球为1人次)参加促销活动，记随机变量η为获得1等奖或2等奖的人次，求P(η＝2)．

在△ABC中，角A，B，C所对的边分别为a，b，c，已知cos2C＝－．

(Ⅰ)求sinC的值；

(Ⅱ)当a＝2，2sinA＝sinC，求b及c的长．

设函数f(x)＝e^x－1－x－ax²．

(Ⅰ)若a＝0，求f(x)的单调区间；

(Ⅱ)若当x≥0时f(x)≥0，求a的取值范围．