经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为：．

(1)若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？

(2)在该时段内，当汽车的平均速度v为多少时，车流量最大？最大车流量为多少？(结果可保留分数形式)

在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，且．

(1)求cosB的值；(2)若b＝，a＋c＝4，求△ABC的面积．

已知数列{a_n}是等差数列，a₁＝1，公差为2，又已知数列{b_n}为等比数列，且b₁＝a₁，b₂(a₂－a₁)＝b₁．

(1)求数列{a_n}、{b_n}的通项公式；(2)设c_n＝，求{c_n}的前n项和S_n．

已知命题p：m＞4；命题q：方程4x²＋4(m－2)x＋9＝0无实根．若p∨q为真，p∧q为假，p为假，求m的取值范围．

已知椭圆的方程为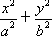＝1(a＞b＞0)，A(0，b)、B(0，－b)和Q(a，0)为的三个顶点．

(1)若点M满足，求点M的坐标；

(2)设直线l₁∶y＝k₁x＋p交椭圆于C、D两点，交直线l₂∶y＝k₂x于点E．若k₁·k₂＝，证明：E为CD的中点；

(3)设点P在椭圆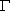内且不在x轴上，如何构作过PQ中点F的直线l，使得l与椭圆的两个交点P₁，P₂满足？令a＝10，b＝5，点P的坐标是(－8，－1)．若椭圆上的点P₁，P₂满足，求点P₁，P₂的坐标．

若实数x、y、m满足|x－m|＜|y－m|，则称x比y接近m．

(1)若x²－1比3接近0，求x的取值范围；

(2)对任意两个不相等的正数a、b，证明：a²b＋ab²比a³＋b³接近2ab；

(3)已知函数f(x)的定义域D＝{x|x≠kπ，k∈Z，x∈R}．任取x∈D，f(x)等于1＋sinx和1－sinx中接近0的那个值．写出函数f(x)的解析式，并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明)．

已知数列{a_n}的前n项和为S_n，且S_n＝n－5a_n－85，n∈N^*．

(1)证明：{a_n－1}是等比数列；

(2)求数列{S_n}的通项公式，并求出使得S_n+1＞S_n成立的最小正整数n．

如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝．再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面)．

(1)当圆柱底面半径r取何值时，S取得最大值？并求出该最大值(结果精确到0.01平方米)；

(2)若要制作一个如图放置的、底面半径为0.3米的灯笼，请作出用于制作灯笼的三视图(作图时，不需考虑骨架等因素)．

已知0＜x＜，化简：lg(cosx·tanx＋1－2sin²)＋lg[cos(x－)]－lg(1＋sin2x)．

已知函数f(x)＝＋x＋(a－1)lnx＋15a，其中a＜0，且a≠－1．

(Ⅰ)讨论函数f(x)的单调性；

(Ⅱ)设函数g(x)＝(e是自然数的底数)．是否存在a，使g(x)在[a，－a]上为减函数？若存在，求a的取值范围；若不存在，请说明理由．