已知函数f(x)＝|x－a|－1nx(a＞0)

(Ⅰ)若a＝1，求f(x)的单调区间及f(x)的最小值；

(Ⅱ)若a＞0，求f(x)的单调区间；

(Ⅲ)证明：＋＋…＋＜(n∈N^*，n≥2)

在下表中，每行上的数从左到右都成等比数列，并且所有公比都等于q，每列上的数从上到下都成等差数列，正数a_ij表示位于第i行第j列的数，其中a₂₄＝，a₄₂＝1，a₅₄＝．

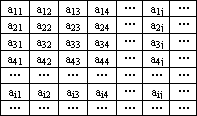
(Ⅰ)求q的值；

(Ⅱ)求a_ij的计算公式；

(Ⅲ)设数列{b_n}满足b_n＝a_nn，{b_n}的前n项和为S_n，试比较S_n与T_n＝(n∈N^*)的大小，并说明理由．

设函数f(x)＝ax²＋bx＋1(a，b∈R)，F(x)＝

(Ⅰ)若f(－1)＝0且对任意实数x均有f(x)≥0成立，求F(x)表达式；

(Ⅱ)在(Ⅰ)的条件下，当x∈[－2，2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围；

(Ⅲ)设m＞0，n＜0，且m＋n＞0，a＞0，f(x)为偶函数，求证F(M)＋F(n)＞0．

如图，四棱锥P－ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，且PA＝2，E为PD中点．

(Ⅰ)求证：PA⊥平面ABCD；

(Ⅱ)求二面角E－AC－D的大小；

(Ⅲ)在线段BC上是否存在点F，使得点E到平面PAF的距离为？若存在，确定点F的位置；若不存在，请说明理由．

某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是，遇到红灯时停留的时间都是2 min．

(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率；

(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间ξ的分布列及期望．

已知函数f(x)＝cos²x－sin²x＋2sinxcosx＋1．

(Ⅰ)求f(x)的最小正周期，并求f(x)的最小值；

(Ⅱ)若f(α)＝2，且α∈[，]，求α的值．

设h(x)＝x＋，x∈[，5]，其中m是不等于零的常数，

(1)m＝1时，直接写出h(x)的值域

(2)求h(x)的单调递增区间；

(3)已知函数f(x)(x∈[a，b])，定义：f₁(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f₂(x)＝max{f(t)|a≤t≤x}(x∈[a，b])．其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值．例如：f(x)＝cosx，x∈[0，π]，则f₁(x)＝cosx，x∈[0，π]，f₂(x)＝1，x∈[0，π]，当m＝1时，|h₁(x)－h₂(x)|≤n恒成立，求n的取值范围；

数列{a_n}的前n项和记为S_n，前kn项和记为

S_kn(n，k∈N^*)，对给定的常数k，若是与n无关的非零常数t＝f(k)，则称该数列{a_n}是“k类和科比数列”，

(1)已知S_n＝a_n－(n∈N^*)，求数列{a_n}的通项公式；

(2)在(1)的条件下，数列a_n＝2^cn，求证数列{c_n}是一个“1类和科比数列”；

(3)、设等差数列{b_n}是一个“k类和科比数列”，其中首项b₁，公差D，探究b₁

与D的数量关系，并写出相应的常数t＝f(k)；

已知F₁(－，0)，F₂(，0)，点P满足||＋||＝4，记点P的轨迹为E，

(1)求轨迹E的方程；

(2)如果过点Q(0，m)且方向向量为＝(1，1)的直线l与点P的轨迹交于A，B两点，当·＝0时，求△AOB的面积．

在△ABC中，已知角A为锐角，且f(A)＝．

(1)将f(A)化简成f(A)＝Msin(wA＋)＋N的形式；

(2)若A＋B＝，f(A)＝1，BC＝2，求边AC的长．；