四棱锥P－ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点．

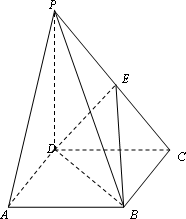
(Ⅰ)证明PA∥平面BDE；

(Ⅱ)求二面角B―DE―C的平面角的余弦值；

(Ⅲ)在棱PB上是否存在点F，使PB⊥平面DEF？若存在，请求出F点的位置；若不存在，请说明理由．

已知函数f(x)＝x＋alnx，其中a为常数，且a≤－1．

(Ⅰ)当a＝－1时，求f(x)在[e，e²](e＝2.718 28…)上的值域；

(Ⅱ)若f(x)≤e－1对任意x∈[e，e²]恒成立，求实数a的取值范围．

某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．

(Ⅰ)若某位顾客消费128元，求返券金额不低于30元的概率；

(Ⅱ)若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X(元)．求随机变量X的分布列和数学期望．

已知函数f(x)＝cos(2x－)＋sin²x－cos²x．

(Ⅰ)求函数f(x)的最小正周期及图象的对称轴方程；

(Ⅱ)设函数g(x)＝[f(x)]²＋f(x)，求g(x)的值域．

选修4－4：坐标系与参数方程

已知曲线C的极坐标方程是ρ＝4cos．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：，求直线l与曲线C相交所成的弦的弦长．

选修4－1：几何证明选讲

如图，在Rt△ABC中，∠C＝90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．

(Ⅰ)求证：AC是△BDE的外接圆的切线；

(Ⅱ)若AD＝2，AE＝6，求EC的长．

已知函数f(x)＝．

(Ⅰ)若函数在区间(a，a＋)(其中a＞0)上存在极值，求实数a的取值范围；

(Ⅱ)如果当x≥1时，不等式f(x)≥恒成立，求实数k的取值范围；

(Ⅲ)求证[(n＋1)！]²＞(n＋1)·e^n－2(n∈N^*)．

如图，设抛物线C₁：y²＝4mx(m＞0)的准线与x轴交于F₁，焦点为F₂；以F₁，F₂为焦点，离心率e＝的椭圆C₂与抛物线C₁在x轴上方的交点为P，延长PF₂交抛物线于点Q，M是抛物线C₁上一动点，且M在P与Q之间运动．

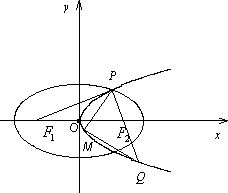
(Ⅰ)当m＝1时，求椭圆C₂的方程；

(Ⅱ)当△PF₁F₂的边长恰好是三个连续的自然数时，求△MPQ面积的最大值．

如图，三棱柱ABC－A₁B₁C₁中，侧面AA₁C₁C⊥底面ABC，AA₁＝A₁C＝AC＝2，AB＝BC，且AB⊥BC，O为AC中点．

(Ⅰ)证明：A₁O⊥平面ABC；

(Ⅱ)求直线A₁C与平面A₁AB所成角的正弦值；

(Ⅲ)在BC₁上是否存在一点E，使得OE∥平面A₁AB，若不存在，说明理由；若存在，确定点E的位置．

某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．

(Ⅰ)若某位顾客消费128元，求返券金额不低于30元的概率；

(Ⅱ)若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X(元)．求随机变量X的分布列和数学期望．