设函数f(x)＝x＋ax2＋blnx，曲线y＝f(x)过P(1，0)，且在P点处的切斜线率为2．

(Ⅰ)求a，b的值；

(Ⅱ)证明：f(x)≤2x－2．

某农场计划种植某种新作物，为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验．选取两大块地，每大块地分成n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙．

(Ⅰ)假设n＝2，求第一大块地都种植品种甲的概率；

(Ⅱ)试验时每大块地分成8小块，即n＝8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位：kg/hm²)如下表：

分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？

附：样本数据x₁，x₂，…，x_a的样本方差s²＝[(x₁－)²＋(x₂－)²＋…＋(x_n－)²]，其中为样本平均数．

如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA＝AB＝PD．

(Ⅰ)证明：PQ⊥平面DCQ；

(Ⅱ)求棱锥Q－ABCD的体积与棱锥P－DCQ的体积的比值．

△ABC的三个内角A，B，C所对的边分别为a，b，c，asinAsinB＋bcos²A＝a．

(Ⅰ)求；

(Ⅱ)若c²＝b²＋a²，求B．

如图，设P是抛物线C₁：x²＝y上的动点．过点P做圆C₂的两条切线，交直线l：y＝－3于A，B两点．

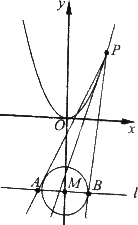
(Ⅰ)求C₂的圆心M到抛物线C₁准线的距离．

(Ⅱ)是否存在点P，使线段AB被抛物线C₁在点P处得切线平分，若存在，求出点P的坐标；若不存在，请说明理由．

设函数f(x)＝a²lnx－x²＋ax，af0

(Ⅰ)求f(x)的单调节器区间

(Ⅱ)求所有实数a，使e－1≤f(x)≤e²对x∈[1，e]恒成立．

注：e为自然对数的底数．

如图，在三棱锥P－ABC中，AB＝AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上．

(Ⅰ)证明：AP⊥BC；

(Ⅱ)已知BC＝8，PO＝4，AO＝3，OD＝2．求二面角B－AP－C的大小．

已知公差不为0的等差数列{a_n}的首项a₁(a₁∈R)，且，，成等比数列．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)对n∈N⁺，试比较与的大小．

已知函数f(x)＝Asin(x＋)，x∈R，A＞0，0＜＜．y＝f(x)的部分图像，如图所示，P、Q分别为该图像的最高点和最低点，点P的坐标为(1，A)．

(Ⅰ)求f(x)的最小正周期及的值；

(Ⅱ)若点R的坐标为(1，0)，，求A的值．

在平面直角坐标系xOy中，已知椭圆．如图所示，斜率为k(k＞0)且不过原点的直线l交椭圆C于A，B两点，线段AB的中点为E，射线OE交椭圆C于点G，交直线x＝－3于点D(－3，m)．

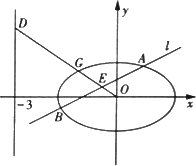
(Ⅰ)求m²＋k²的最小值；

(Ⅱ)若|OG|²＝|OD|·|OE|，

(i)求证：直线l过定点；

(ii)试问点B，G能否关于x轴对称？若能，求出此时△ABG的外接圆方程；若不能，请说明理由．