(上海)在平面上，两条直线的位置关系有相交、平行、重合三种．已知α，β是两个相交平面，空间两条直线l₁，l₂在α上的射影是直线s₁，s₂，l₁，l₂在β上的射影是直线t₁，t₂．用s₁与s₂，t₁与t₂的位置关系，写出一个总能确定l₁与l₂是异面直线的充分条件：________

已知函数y＝kx与y＝x²＋2(x≥0)的图象相交于A(x₁，y₁)，B(x₂，y₂)，l₁，l₂分别是y＝x²＋2(x≥0)的图象在A，B两点的切线，M，N分别是l₁，l₂与x轴的交点．

(Ⅰ)求k的取值范围；

(Ⅱ)设t为点M的横坐标，当x₁＜x₂时，写出t以x₁为自变量的函数式，并求其定义域和值域；

(Ⅲ)试比较|OM|与|ON|的大小，并说明理由(O是坐标原点)．

某商场经销某商品，根据以往资料统计，顾客采用的付款期数ξ的分布列为

商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为

250元；分4期或5期付款，其利润为300元．η表示经销一件该商品的利润．

(Ⅰ)求事件A：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率P(A)；

(Ⅱ)求η的分布列及期望Eη．

猎人在距离100米处射击一野兔，其命中率为0.5，如果第一次射击未中，则猎人进行第二次射击，但距离150米．如果第二次射击又未中，则猎人进行第三次射击，并且在发射瞬间距离为200米．已知猎人的命中概率与距离的平方成反比，求猎人命中野兔的概率．

某单位有三辆汽车参加某种事故保险，单位年初向保险公司缴纳每辆900元的保险金．对在一年内发生此种事故的每辆汽车，单位获9000元的赔偿(假设每辆车最多只赔偿一次)．设这三辆车在一年内发生此种事故的概率分别为

假设每一架飞机引擎飞机中故障率为P，且个引擎是否发生故障是独立的，如果有至少50％的引擎能正常运行，问对于多大的P而言，4引擎飞机比2引擎飞机更安全？

甲、乙、丙3人投篮，投进的概率分别是，，．

(Ⅰ)现3人各投篮1次，求3人都没有投进的概率；

(Ⅱ)用ξ表示乙投篮3次的进球数，求随机变量ξ的概率分布及数学期望Eξ．

某批产品成箱包装，每箱5件．一用户在购进该批产品前先取出3箱，再从每箱中任意抽取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品．

(Ⅰ)用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；

(Ⅱ)若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品级用户拒绝的概率．

在平面直角坐标系中，O为坐标原点，已知点M(1，－3)，N(5，1)，若点C满足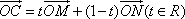，点C的轨迹与抛物线y²＝4x交于A、B两点；

(1)求点C的轨迹方程；

(2)求证：；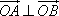

(3)在x轴正半轴上是否存在一定点P(m，0)，使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍，若存在，求出m的值；若不存在，请说明理由．

已知射线OA、OB的方程分别为，，动点M、N分别在OA、OB上滑动，且．

(1)若，求P点的轨迹C的方程；

(2)已知，，请问在曲线C上是否存在动点P满足条件，若存在，求出P点的坐标，若不存在，请说明理由．