某地区试行高考考试改革：在高三学年中举行5次统一测试，学生如果通过其中2次测试即可获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加5次测试．假设某学生每次通过测试的概率都是，每次测试通过与否相互独立．规定：若前4次都没有通过测试，则第5次不能参加测试．

(1)求该学生考上大学的概率；

(2)如果考上大学或参加完5次考试就结束，记该生参加测试的次数为ξ，求ξ的分布列及数学期望Eξ

已知A，B，C为锐角△ABC的三个内角，向量＝(2－sinA，cosA－sinA)，＝(1＋sinA，cosA－sinA)，且⊥．

(1)求A的大小；

(2)求y＝2sin²B＋cos(－2B)取最大值时，B的大小．

函数在x＝1处取得极值，的最小值为－4．

(1)求m，n的值及f(x)的单调区间；

(2)试分别求方程f(x)－c＝0在区间[－4，1]上有一根、有两根时c的范围．

已知数列{a_n}中，，且．

(1)令b_n＝2ⁿa_n，求数列{b_n}的通项公式；

(2)令，求数列{c_n}的前n项和S_n．

某地区试行高考考试改革：在高三学年中举行5次统一测试，学生如果通过其中2次测试即可获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加5次测试．假设某学生每次通过测试的概率都是，每次测试通过与否相互独立．规定：若前4次都没有通过测试，则第5次不能参加测试．

(1)求该学生考上大学的概率；

(2)如果考上大学或参加完5次考试就结束，求该生至少参加四次考试的概率．

已知A，B，C为锐角△ABC的三个内角，向量，，且．

(1)求A的大小；

(2)求取最大值时，B的大小．

选修4－1：几何证明选讲

如图，ΔABCD内接于⊙O，AB＝AC，直线MN切⊙O于点C，弦BD∥MN，AC与BD相交于点E．

(Ⅰ)求证：ΔABE≌ΔACD；

(Ⅱ)若AB＝6，BC＝4，求AE．

已知椭圆，过点的直线与原点的距离为．

(Ⅰ)求椭圆E的方程；

(Ⅱ)直线与椭圆E交于C、D两点，以线段CD为直径的圆过点M(－1，0)，求直线l的方程．

已知函数f(x)＝x²＋alnx

(Ⅰ)当的单调区间和极值；

(Ⅱ)若函数在[1，4]上是减函数，求实数a的取值范围．

甲乙两个学校高三年级分别有1100人，1000人，为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况，采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩，并作出了频数分布统计表如下：

甲校：

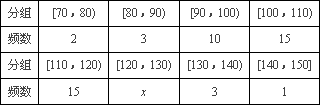
乙校：

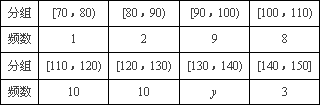
(Ⅰ)计算x，y的值．

(Ⅱ)若规定考试成绩在[120，150]内为优秀，请分别估计两个学校数学成绩的优秀率；

(Ⅲ)由以上统计数据填写下面2×2列联表，并判断是否有97.5％的把握认为两个学校的数学成绩有差异．

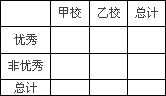
附：K²＝；