已知椭圆C的中心在圆点，焦点在x轴上，F₁，F₂分别是椭圆C的左、右焦点，M是椭圆短轴的一个端点，过F₁的直线l与椭圆交于A，B两点，△MF₁F₂的面积为4，△ABF₂的周长为

(Ⅰ)求椭圆C的方程；

(Ⅱ)设点Q的坐标为(1，0)，是否存在椭圆上的点P及以Q为圆心的一个圆，使得该圆与直线PF₁，PF₂都相切，若存在，求出P点坐标及圆的方程；若不存在，请说明理由．

如图所示，已知△AOB中，AB＝2OB＝4，D为AB的中点，若△AOC是△AOB绕直线AO旋转而成的，记二面角B－AO－C的大小为．

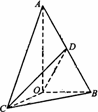
(Ⅰ)若，求证：平面COD⊥平面AOB；

(Ⅱ)若时，求二面角C－OD－B的余弦值的最小值．

2010年广东亚运会，某运动项目设置了难度不同的甲、乙两个系列，每个系列都有K和D两个动作，比赛时每位运动员自选一个系列完成，两个动作得分之和为该运动员的成绩．假设每个运动员完成每个系列中的两个动作的得分是相互独立的，根据赛前训练统计数据，某运动员完成甲系列和乙系列的情况如下表：

甲系列：

乙系列：

现该运动员最后一个出场，其之前运动员的最高得分为118分．

(Ⅰ)若该运动员希望获得该项目的第一名，应选择哪个系列，说明理由，并求其获得第一名的

概率；

(Ⅱ)若该运动员选择乙系列，求其成绩X的分布列及其数学期望EX．

已知函数f(x)＝xlnx．

(Ⅰ)求函数上的最小值；

(Ⅱ)求证：对一切x∈(0，＋∞)，都有

已知函数

(Ⅰ)求函数f(x)的最小正周期和值域；

(Ⅱ)记△ABC的内角A、B、C的对边分别是a，b，c，若求角C的值．

在直三棱柱ABC－A₁B₁C₁中，∠ACB＝90°，AC＝BC＝AA₁＝1，D、E分别为棱AB、BC的中点，M为棱AA₁上的点．

(1)证明：A₁B₁⊥C₁D；

(2)当的大小．

已知函数f(x)＝lnx，g(x)＝x²－2x．

(1)设h(x)＝f(x＋1)－(x)(其中(x)是g(x)的导函数)，求h(x)的最大值；

(2)证明：当0＜b＜a时，求证：f(a＋b)－f(2a)＜；

(3)设k∈Z，当x＞1时，不等式k(x－1)＜xf(x)＋3(x)＋4恒成立，求k的最大值．

已知椭圆C：＋＝1(a＞b＞0)的离心率为，短轴一个端点到右焦点的距离为．

(1)求椭圆C的方程；

(2)设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为，求△AOB面积的最大值．

设数列{a_n}的前n项和为S_n，点(S_n，a_n)在直线(3－m)x＋2my―m―3＝0上，(m为常数，m∈N^*，m≠3)．

(1)求a_n；

(2)若数列{a_n}的公比q＝f(m)，数列{b_n}满足b₁＝a₁，，，求证：为等差数列，并求b_n；

(3)设数列{c_n}满足c_n＝b_n·b_n+2，T_n为数列{c_n}的前n项和，且存在实数T满足，求T的最大值．

将10个白小球中的3个染成红色，3个染成黄色，试解决下列问题：

(1)求取出3个小球中红球个数ξ的分布列和数学期望；

(2)求取出3个小球中红球个数多于白球个数的概率．