(1)求f(x)的最小值；

(2)不等式f(x)＞ax的解集为P，若求实数a的取值范围；

(3)已知，是否存在等差数列{a_n}和首项为f(1)公比大于0的等比数列{b_n}，使数列{a_n＋b_n}的前n项和等于S_n

如图，椭圆长轴端点为A，B，O为椭圆中心，F为椭圆的右焦点，且，．

(1)求椭圆的标准方程；

(2)记椭圆的上顶点为M，直线l交椭圆于P，Q两点，问：是否存在直线l，使点F恰为△PQM的垂心？若存在，求出直线l的方程；若不存在，请说明理由．

如图，在三棱锥P－ABC中，PA⊥底面ABC，PA＝AB，∠ABC＝60°，∠BCA＝90°，点D、E分别在棱PB，PC上，且DE∥BC

(Ⅰ)求证：BC⊥平面PAC；

(Ⅱ)当D为PB的中点时，求AD与平面PAC所成角的大小的余弦值；

(Ⅲ)是否存在点E，使得二面角A―DE―P为直二面角？并说明理由．

A处一缉私艇发现在北偏东45°方向，距离12 n mile的海面C处有一走私船正以10 n mile/h的速度沿东偏南15°方向逃窜．缉私艇的速度为14 n mile/h，若要在最短的时间内追上该走私船，缉私艇应沿北偏东45°＋α的方向去追，求追击所需的时间和α角的正弦值．

已知函数(其中)

(Ⅰ)求函数f(x)的值域；

(Ⅱ)若对任意的a∈R，函数y＝f(x)，x∈(a，a＋π]的图象与直线y＝－1有且仅有两个不同的交点，试确定的值(不必证明)，并求函数y＝f(x)，x∈R的单调增区间

数列上，

(1)求数列{a_n}的通项公式；

(2)若

已知函数f(x)＝的图象过坐标原点O，且在点(－1，f(－1))处的切线的斜率是－5．

(1)求实数b、c的值；

(2)求f(x)在区间[－1，2]上的最大值

某单位建造一间地面面积为12平方米的背面靠墙的矩形小房，由于地理位置的限制，房子侧面的长度x不得超过a米，房屋正面的造价为400元/平方米，房屋侧面的造价为150元/平方米，屋顶和地面的造价费用合计为5800元，如果墙高为3米，且不计房屋背面的费用．

(1)把房屋总造价y表示成x的函数，并写出该函数的定义域；

(2)当侧面的长度为多少时，总造价最低？最低造价是多少？

如图，菱形ABCD的边长为6，∠BAD＝60°，AC∩BD＝0．将菱形ABCD沿对角线AC折起，得到三棱锥B－ACD，点M是棱BC的中点，．

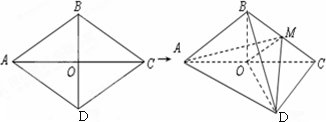
(1)求证：OM∥平面ABD；

(2)求证：OD⊥平面ABC；平面MDO⊥平面ABC；

(3)求三棱锥M－ABD的体积．

已知函数最小正周期为．

(1)求的值及函数f(x)的解析式；

(2)若△ABC的三条边a，b，c满足a²＝bc，a边所对的角为A．求角A的取值范围及函数f(A)的值域．