已知平面区域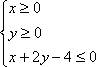恰好被面积最小的圆C：(x－a)²＋(y－b)²＝r²及其内部所覆盖．

(1)试求圆C的方程．

(2)是否存在斜率为1的直线l与圆C交于不同两点A、B，使得以AB为直径的圆经过点P(1，0)，若存在，求出直线l的方程，若不存在，说明理由．

已知数列{a_n}满足a₁＋a₂＋…＋a_n＝4a_n－p(n∈N^*)，其中p是不为零的常数

(1)证明：数列{a_n}为等比数列；

(2)当p＝3时，若数列{b_n}满足b_n+1＝a_n＋b_n(n∈N^*)，b₁＝2求数列{b_n}的通项公式；

已知函数f(x)＝2cosωx(sinωx＋cosωx)(其中ω＞0)，且函数f(x)的图象的相邻两条对称轴间的距离为π．

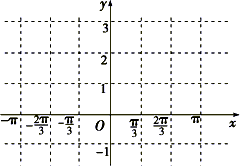
(1)先列表，再作出函数f(x)在区间[－π，π]上的图象；

(2)若f()＝2，求cos(－x)的值；

(3)在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cosB＝bcosC，求函数f(A)的取值范围．

如图，A是单位圆与轴正半轴的交点，点B、P在单位圆上，且B(－)∠AOB＝α，∠AOP＝(0＜＜π)，＝＋，四边形OAQP的面积为S．

(1)求cosα＋sinα；

(2)求·＋S的最大值及此时的值₀．

已知函数f(x)＝

(1)求函数f(x)的单调区间；

(2)设函数g(x)＝xf(x)＋t(x)＋e^－x(t∈R)，是否存在实数a，b，c∈[0，1]，使得g(a)＋g(b)＜g(c)？若存在，求出t的取值范围；若不存在，说明理由．

函数f(x)＝－x³＋3x²，设g(x)＝6lnx－(x)(其中(x)为f(x)的导函数)，若曲线y＝g(x)在不同两点A(x₁，g(x₁))、B(x₂，g(x₂))处的切线互相平行，且≥m恒成立，求实数m的最大值．

如图△ABC为正三角形，边长为2，以点A为圆心，1为半径作圆，PQ为圆A的任意一条直径．

(1)若，求||；

(2)求的最小值．

(2)判断＋的值是否会随点P的变化而变化，请说明理由．

对于给定数列{a_n}，如果存在实常数p，q，使得a_n＋1＝pa_n＋q对于任意n∈N^*都成立，我们称数列{a_n}是“M类数列”．

(Ⅰ)已知数列{b_n}是“M类数列”且b_n＝2n，求它对应的实常数p，q的值；

(Ⅱ)若数列{c_n}满足c₁＝1，c_n＋1－c_n－2ⁿ(n∈N^*)，求数列{c_n}的通项公式．并判断{c_n}是否为“M类数列”，请说明理由．

在△ABC中，角A，B，C所对的边分别为a，b，c，λc＝2acosB(λ∈R)．

(Ⅰ)当λ＝1时，判断△ABC的形状；

(Ⅱ)若B＝60°，2b²＝3ac，求λ的值．

已知a∈R，函数f(x)＝lnx－1，g(x)＝(lnx－1)e^x＋x(其中e为自然对数的底数)．

(1)判断函数f(x)在(0，e]上的单调性；

(2)是否存在实数x₀∈(0，＋∞)，使曲线y＝g(x)在点x＝x₀处的切线与y轴垂直？若存在，求出x₀的值；若不存在，请说明理由．

(3)若实数m，n满足m＞0，n＞0，求证：nⁿe^m≥mⁿeⁿ．