选修4－4：作标系与参数方程．

已知直线l的参数方程为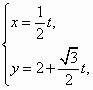(t为参数)，曲线C的极坐标方程为，以极点为原点，极轴为x轴正半轴建立直角坐标系，M点坐标为(0，2)，直线L与曲线C交于A，B两点．

(1)写出直线L的普通方程和曲线C的直角坐标方程．

(2)求线段MA，MB的长度之积|MA|·|MB|．

选修4－1：几何证明选讲

如图，⊙O是△ABC的外接圆，D是弧AC的中点，BD交AC于E．

(Ⅰ)求证：CD²＝DE·DB．

(Ⅱ)若O到AC的距离为1，求⊙O的半径．

(文)已知函数，其中a＞0．

(Ⅰ)若a＝1，求曲线y＝f(x)在点(2，f(2))处的切线方程；

(Ⅱ)若在区间上，f(x)＞0恒成立，求a的取值范围．

(理)已知a∈R，函数(其中e≈2.718)

(Ⅰ)求函数f(x)在区间(0，e]上的最小值；

(Ⅱ)是否存在实数x₀∈(0，e]，使曲线y＝g(x)在点x＝x₀处的切线与y轴垂直？若存在，求出x₀的值；若不存在，请说明理由．

已知F₁(－c，0)，F₂(c，0)是椭圆的左、右焦点，过点F₁作倾斜角为60°的直线l交椭圆于A，B两点，△ABF₂的内切圆的半径为

(Ⅰ)求椭圆的离心率；

(Ⅱ)若，求椭圆的标准方程．

为了调查某中学高三学生的身高情况，在该中学高三学生中随机抽取了40名同学作为样本，测得他们的身高后，画出频率分布直方图如下：

(Ⅰ)求身高在180～190 cm之间的人数．

(Ⅱ)从身高在180 cm(含180 cm)以上的样本中随机抽取2人，(理)记身高在185～190 cm之间的人数为X，求X的分布列和数学期望．

(文)求至少有一人身高在185～190 cm之间的概率．

如图，正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD，AE⊥平面CDE．

(Ⅰ)求证：AB⊥平面ADE；

(Ⅱ)(理)在线段BE上存在点M，使得直线AM与平面EAD所成角的正弦值为，试确定点M的位置．

(文)若AD＝2，求四棱锥E－ABCD的体积．

在△ABC中，已知内角，边．设内角B＝x，周长为y．

(1)求函数y＝f(x)的解析式；

(2)求y的最大值．

已知函数

(1)讨论f(x)的单调区间；

(2)若对任意的x₁∈[1，＋∞)，总存在成立，求a的取值范围．

已知，B、D是圆上两动点，且四边形ABCD是矩形

(1)求顶点C的轨迹E的方程；

(2)若过点F(2，0)作曲线E的互相垂直的弦PQ和MN，求四边形PMQN面积的最大值和此时弦所在的直线方程．