函数f(x)＝cos²ωx＋sinωxcosωx，其中ω＞0，且f(x)的图像在y轴右侧第一个最高点的横坐标为．

(Ⅰ)求f(x)的解析式；

(Ⅱ)由y＝sinx的图象，经过怎样的变换，可以得到f(x)的图象？

选修4－5：不等式选讲

已知f(x)＝|x＋1|＋|x－1|，不等式f(x)＜4的解集为M．

(1)求M；

(2)当a，b∈M时，证明：2|a＋b|＜|4＋ab|

选修4－4：坐标系与参数方程

已知曲线C₁的参数方程为(为参数)，曲线C₂的参数方程为(t为参数)，且曲线C₁与C₂相交于A，B两点．

(1)求曲线C₁，C₂的普通方程；

(2)若点，求△FAB的周长．

已知，g(x)＝log_ax(a＞0且a≠1)．

(1)过P(0，2)作曲线y＝f(x)的切线，求切线方程；

(2)设h(x)＝f(x)－g(x)在(0，＋∞)上为减函数，且其导函数存在零点，求实数a的值．

已知椭圆E经过点A(2，3)，对称轴为坐标轴，焦点F₁，F₂在x轴上，离心率．

(1)求椭圆E的方程；

(2)求∠F₁AF₂的平分线所在直线l的方程；

(3)在椭圆E上是否存在关于直线l对称的相异两点？若存在，请找出；若不存在，说明理由．

某校高三某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图，据此解答如下问题：

(1)求分数在[50，60]的频率及全班的人数；

(2)求分数在[80，90)之间的频数，并计算频率分布直方图中[80，90)间的矩形的高；

(3)若要从分数在[80，100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份在[90，100]之间的概率．

如图，某市拟在长为8 km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数的图象，且图象的最高点为；赛道的后一部分为折线段MNP．为保证参赛运动员的安全，限定∠MNP＝120°．

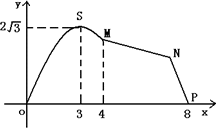
(1)求A，ω的值和M，P两点间的距离；

(2)应如何设计，才能使折线段线段MNP最长？

选修4－5：不等式选讲

已知f(x)＝|x＋1|＋|x－1|，不等式f(x)＜4的解集为M．

(1)求M；

(2)当a，b∈M时，证明：2|a＋b|＜|4＋ab|

选修4－4：坐标系与参数方程

已知曲线C₁的参数方程为(为参数)，曲线C₂的参数方程为(t为参数)，且曲线C₁与C₂相交于A，B两点．

(1)求曲线C₁，C₂的普通方程；

(2)若点，求△FAB的周长．

已知函数．

(1)求f(x)的单调区间；

(2)若对于任意的x∈(0，＋∞)，都有，求k的取值范围．