已知椭圆C₁：的右顶点为P(1，0)，过C₁的焦点且垂直长轴的弦长为1．

(I)求椭圆C₁的方程；

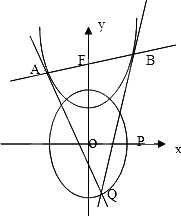
(II)设抛物线C₂：y＝x²＋h(h∈R)的焦点为F，过F点的直线l交抛物线与A、B两点，过A、B两点分别作抛物线C₂的切线交于Q点，且Q点在椭圆C₁上，求△ABQ面积的最值，并求出取得最值时的抛物线C₂的方程．

，定义，其中n∈N*．

(Ⅰ)求a₁，a₂的值，并求证：数列{a_n}是等比数列；

(Ⅱ)若，其中n∈N*，试比较9T_2n与Q_n大小，并说明理由．

在△ABC中，a，b，c分别为内角A，B，C所对的边，A＜B＜C，A，B，C成等差数列，公差为，且也成等差数列．

(Ⅰ)求；

(Ⅱ)若，求⊿ABC的面积．

已知f(x)＝ax²(a∈R)，g(x)＝2lnx

(1)讨论函数F(x)＝f(x)－g(x)的单调性

(2)若方程f(x)＝g(x)在区间[ ，e] 上有两个不等解，求a的取值范围

设数列{a_n}的前项和为S_n，对任意的n∈N^*点(n，)均在直线y＝3x－2上，

(1)求数列{a_n}的通项公式；

(2)设是数列b_n＝，T_n是其前n项和，求使T_n≤对所有n∈N^*都成立的最小正整数m．

定义在R上的增函数y＝f(x)对于任意x，yÎ R都有f(x＋y)＝f(x)＋f(y)

(1)求f(0)

(2)求证：f(x)为奇函数

(3)若f(3^xk)＋f(3^x－9^x－2)＜0对任意xÎ R恒成立，求实数k的取值范围

△ABC三内角A，B，C的对边分别为a，b，c，向量＝(2sinA，－)，＝(cos2A，2cos²－1)，且∥，

(1)求锐角A的大小；

(2)a＝4，求△ABC面积的最大值．

某工厂统计资料显示，产品次品率p与日产量x(单位：件， x∈Î N^*，1≤x≤96)的关系如下：

又知每生产一件正品盈利a(a为正常数)元，每生产一件次品就损失元

(1)将该厂日盈利额T(元)表示为日产量x的函数．

(2)为了获得最大的盈利，该厂的日产量应定为多少件？(注：次品率p＝×100％，正品率＝1－p)．

定义在R上的增函数y＝f(x)对于任意x，yÎ R都有f(x＋y)＝f(x)＋f(y)

(1)求f(0)．

(2)求证：f(x)为奇函数．

(3)若f(3^xk)＋f(3^x－9^x－2)＜0对任意xÎ R恒成立，求实数k的取值范围．

深圳市某校中学生篮球队假期集训，集训前共有6个篮球，其中3个是新球(即没有用过的球)，3个是旧球(即至少用过一次的球)．每次训练，都从中任意取出2个球，用完后放回．

(1)设第一次训练时取到的新球个数为ξ，求ξ的分布列和数学期望；

(2)求第二次训练时恰好取到一个新球的概率．